Конструкция - решение
Cтраница 1
Конструкция решения ( 6) представлена в виде суперпозиции двух независимых решений, соответствующих нормальной и касательной нагрузкам интенсивностью р ( р), q ( p) ( 4), причем их трансформанты Ханкеля р ( ( 3), q ( ( 3) ( 5) вынесены в качестве множителей под знаками интегралов. Удовлетворяя в решении ( 6) краевым условиям ( 1), ( 2) или ( 1), ( 3) отдельно при р ( р) 0, q ( p) 0 и при р ( р) О, q ( p) 0, приходим к замкнутым системам функциональных уравнений ( СФУ) 47V 2 порядка для определения полного набора неизвестных функций Aki ( ( 3), Bki ( / 3), Cki ( / 3), Dki ( fi) ( i l N) AkN l ( fi), BkN l ( fi) на полуоси 0 J3 оо соответственно при нормальной ( k р) и касательной ( k q) нагрузках. Функциональные матрицы СФУ зависят только от конструкции многослойного полупространства и не зависят от трансформант Ханкеля p ( j3), q (), которые в первой основной краевой задаче известны, а во второй основной и смешанной краевых задачах неизвестны и подлежат определению соответственно из однородных и смешанных краевых условий. [1]
Ключом к геометрическому пониманию конструкции решений, инвариантных относительно группы, является выяснение структуры соответствующих подмножеств пространства струй. [2]
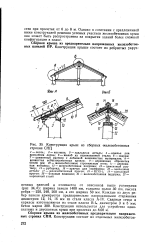 |
Конструкция крыш из сборных железобетонных стропил СНГ ]. [3] |
Однако в сочетании с предложенной ниже конструкцией решения угловых участков железобетонных крыш она может быть распространена на покрытия зданий более сложной конфигурации в плане. [4]
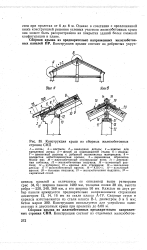 |
Конструкция крыш из сборных железобетонных стропил СНП. [5] |
Однако в сочетании с предложенной НИЖЕ конструкцией решения угловых участков железобетонных крыш она может быть распространена на покрытия зданий более сложной конфигурации в плане. [6]
Покажем, что даже в частном случае конструкция решения (2.4) уравнения (1.1) приводит к содержательному, как нам представляется, результату. [7]
Тот факт, что внешние задачи оказались разрешимыми в потенциалах для всех значений параметра со2, указывает на возможность априорной конструкции решения в таком виде, который приводит к интегральным уравнениям, разрешимым по первой теореме Фредгольма. Однако в общем случае разыскание подобных искусственных конструкций затруднительно, и, как мы видели, в этом нет никакой необходимости. Достаточно каждый раз пользоваться потенциалами либо простого, либо двойного слоя и хотя при этом приходим, вообще говоря, к необходимости обращаться к третьей теореме Фредгольма, но интегральные уравнения сами указывают тот набор функций, которые обеспечивают разрешимость. [8]
Решение по этой схеме, вообще говоря, может отличаться от решения такой же упруго-пластической задачи при модуле Юнга Е - сю. Выделение жестких зон в известной мере произвольно, а напряжения в них не определены. С этим связано характерное для жестко-пластического тела отсутствие единственности конструкции решения и некоторые другие парадоксальные заключения. [9]
При этом подчеркивалось, что в одном графике может содержаться значительное количество информации. Однако затем с помощью этого метода была легко получена и конструкция решения, а также установлена стационарность минимума. [10]
В монографии [32] получены сложные для практического использования зависимости. В реальных конструкциях передача локальных нагрузок или сосредоточенных сил обычно осуществляется через жесткое включение. При этом в месте их сопряжения действуют большие напряжения, связанные в основном с изгибом. В работе [21 ] получены простые для таких конструкций решения для основных встречающихся на практике схем нагружения, которые достаточно точно определяют усилия в местах сопряжений с жестким включением и прилегающих к ним зонах. [11]
Страницы: 1