Конструкция - цепь
Cтраница 1
Конструкция цепи и профиль зуба звездочки допускают минимальное число зубьев: для зубчатых цепей гш. Однако данные числа зубьев звездочки не обеспечивают надежной работы цепного привода и поэтому могут применяться в исключительных случаях для маломощных и тихоходных передач, а также для паразитных ( регулирующих) звездочек. [1]
 |
Конструктивные типы изоляции токопроводящих жил. [2] |
Конструкция цепи в любом поперечном сечении имеет ось симметрии. [3]
 |
Кабеленесущие цепи, смонтированные на суппортах тяжелого токарного станка. [4] |
Конструкция цепей обеспечивает только определенные минимальные радиусы изгибов кабелей, что предотвращает преждевременный выход их из строя или нарушение изоляции отдельных жил. Возможность одновременного прокладывания вместе с электрическими кабелями и проводами шлангов для подвода масла в гидросистемах и охлаждающей жидкости, придает станку опрятный вид, снижает скопление грязи возле него и упрощает обслуживание станка. [5]
Конструкции цепей улучшаются с каждым годом. [6]
Конструкция цепи должна отвечать жестким требованиям, поскольку она должна быть переведена с помощью устройства программирования ( транслятора) в последовательность выполняемых команд. Формат цепи может быть фиксированным или переменным. В первом случае цепь должна состоять из определенного числа компонентов. Символ присваивания позволяет идентифицировать строку программы и назначить промежуточную переменную или соответствующий выход. [7]
Конструкция другой бесшумной цепи показана на фиг. [8]
Элементом конструкции цепи являются так называемые обратные провода, замыкающие цепь. [9]
При двухцепной конструкции цепи прикрепляются к скребкам по бокам, а при одноцеп-ной - посредине. [10]
 |
Канатно-дисковые скребковые конвейеры. [11] |
При двухцепной конструкции цепи прикрепляются к скребкам по краям, а при одноцепной - посередине. [12]
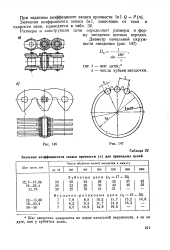 |
Значения коэффициентов запаса прочности [ п ] для приводных цепей. [13] |
Размеры и конструкция цепи определяют размеры и форму звездочек цепных передач. [14]
В этой конструкции цепи и коцепи определяются независимо посредством перехода соответственно к обратному и прямому пределам по некоторой специальной системе покрытий. В категории локально конечных полиэдров возникающая теория эквивалентна классическим гомологиям и когомологиям второго рода. Для конечно порожденных коэффициентов теория гомологии изоморфна теории Бореля - Мура. Описание конструкции элементарно в том смысле, что укладывается в стандартные рамки теории цепных комплексов. Однако цепи и коцепи автоматически совпадают с сечениями определяемых ими вялых и мягких дифференциальных пучков, что позволяет оперировать средствами теории пучков без каких-либо искусственных ограничений. Это проявляется, например, в доказательстве двойственности Пуанкаре - Лефшеца, которая устанавливается при минимальных предположениях и без ограничений на коэффициенты. [15]
Страницы: 1 2 3 4