Последняя асимптота

Cтраница 1

Асимптотические ЛАЧХ ( к примеру. г. 0 ( a. v. [1]

Последняя асимптота представляет прямую, которая начинается с конца асимптоты, закачивающейся на последней сопрягающей частоте, и уходит в бесконечность. [2]

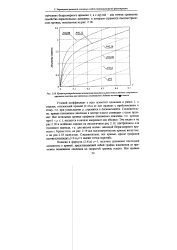Кривые распределения понижения давления в различных точках закрытого кругового пласта при заданном постоянном дебите точечнщр стока. [3]

Полагая в формуле ( 2.41 а) р1, получим уравнение последней асимптоты к кривой, представляющей собой график изменения со временем понижения давления на закрытой границе пласта. [4]

Сопрягающая частота ш % обусловлена элементарным множителем 0 01 s2 - - 0 1 s - - 1, расположенным в знаменателе. Поэтому наклон последней, четвертой асимптоты отличается от наклона третьей асимптоты на - 40 дБ / дек и составляет - 40дБ / дек. Последнюю асимптоту проводим от конца третьей асимптоты до бесконечности. [5]

Для построения асимптотической логарифмической ам-плитудночастотной характеристики проводят прямую через точку с ординатой 0 дб. Эта прямая с наклоном 0 дб на декаду аппроксимирует амплитудночастотную характеристику pslsp разомкнутой системы для интервала низких частот. По достижении сопрягающей частоты сол величина p8 / sp начинает испытывать влияние первой постоянной времени tR звена 1 ( тл / и 1) и аппроксимируется далее асимптотой be, наклон которой составляет-20 дб на декаду. Проводится последняя асимптота cd с наклоном-40 дб на декаду. Истинная частотная характеристика pslsp смещена вниз от точки с ( абсцисса которой равна сопрягающей частоте со) асимптоты cd на 3 дб. Октавой ниже и октавой выше от точки, соответствующей сопрягающей частоте, истинная характеристика проходит под асимптотой на расстоянии 1 дб. Таким образом, истинная амплитудночастотная характеристика легко находится после проведения асимптот. Фазочастотная характеристика строится с учетом того, что полный угол сдвига фаз ф ( / со) представляет собой сумму трех сотавляющих ( рч. [6]

Страницы: 1