Диаграмма - стационарное решение
Cтраница 1
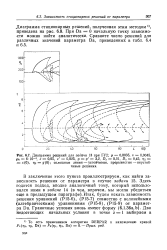
Диаграмма стационарных решений, полученная этим методом 1, приведена на рис. 6.8. При Da 0 начальную точку зависимости можно найти аналитически. [2]
На диаграмме стационарных решений обычно указывается и характер устойчивости этих решений, при этом сплошной линией мы изображаем ветви устойчивых стационарных решений, а пунктирной линией ветви неустойчивых стационарных решений. Изменение характера устойчивости происходит обыкновенно в точках поворота и в точках ветвления. [3]
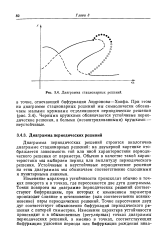 |
Диаграмма стационарных решений. [4] |
Диаграмма периодических решений строится аналогично диаграмме стационарных решений: на двумерной картинке отображается зависимость той или иной характеристики периодического решения от параметра. Обычно в качестве такой характеристики мы выбираем период или амплитуду периодического решения. Устойчивые и неустойчивые периодические решения на этих диаграммах мы обозначаем соответственно сплошными: и пунктирными линиями. [5]
Случай а) соответствует точке ветвления на диаграмме стационарных решений. Зависимость х ( а) в точке а претерпевает излом. В случае Ь) ( бифуркация типа вилки) решение продолжается по одной из последующих устойчивых ветвей, выбранных случайным образом в зависимости от погрешностей аппроксимации и округления. В реальных физических или биологических проблемах удобно рассматривать соответствующую задачу как стохастическую; характер распределения флуктуации переменных состояния определяет тогд а вероятности выбора отдельных ветвей решения. [6]
В некоторых случаях оказывается возможным достаточно быстро построить диаграмму стационарных решений, если к выбранному значению некоторого начального условия с помощью интегрирования задачи Коши мы добавим соответствующее значение параметра. Так же, как и там, возможность применения этого подхода зависит от конкретного вида дифференциальных уравнений и граничных условий, а также от того, как входит в уравнения выбранный параметр. [7]
При параметрическом исследовании выбранной задачи нас обычно интересуют все ветви на диаграмме стационарных решений. [8]
Результаты, полученные с помощью указанного метода линеаризации, были использованы для выделения областей устойчивости на диаграммах стационарных решений, приведенных в § 5.2. Покажем, как подсчитываются значения К и К2 в табл. 5.2. Дифференцируя по соответствующим переменным правые части дифференциальных уравнений задачи 1, мы получаем ( ср. [9]
Результаты последовательного использования метода Ньютона для системы разностных уравнений (6.1.23), которая возникает в задаче 17, представлены на диаграмме стационарных решений, показанной на рис. 6.2. В данном случае уже само решение системы (6.1.23) для больших п являлось достаточно серьезной проблемой. [10]
Устойчивость стационарного решения системы (5.1.1) характеризуется собственными числами матрицы Якоби, определяемой правыми частями соответствующих уравнений. Если мы изменяем один из параметров системы, то вдоль ветви решения на соответствующей диаграмме решений характер устойчивости может изменяться лишь в точках, где собственное число переходит из левой половины комплексной плоскости в правую. Переход вещественного собственного числа через нуль обсуждался нами в § 5.2. Если пара комплексно-сопряженных собственных чисел пересекает мнимую ось, то матрица Якоби все время остается невырожденной, и на диаграмме стационарных решений мы имеем регулярную точку данной ветви. Точки диаграммы стационарных решений, в которых пара комплексно-сопряженных собственных чисел пересекает мнимую ось, называются точками комплексной бифуркации1) или точками бифуркации Хопфа, по имени математика, опубликовавшего одну из основополагающих работ о характере решений в окрестности таких точек. Следующий существенный факт мотивирует разработку алгоритмов для нахождения точек комплексной бифуркации: в указанных точках ( при выполнении определенных условий) от ветви стационарных решений отходит ветвь периодических решений. [11]
Устойчивость стационарного решения системы (5.1.1) характеризуется собственными числами матрицы Якоби, определяемой правыми частями соответствующих уравнений. Если мы изменяем один из параметров системы, то вдоль ветви решения на соответствующей диаграмме решений характер устойчивости может изменяться лишь в точках, где собственное число переходит из левой половины комплексной плоскости в правую. Переход вещественного собственного числа через нуль обсуждался нами в § 5.2. Если пара комплексно-сопряженных собственных чисел пересекает мнимую ось, то матрица Якоби все время остается невырожденной, и на диаграмме стационарных решений мы имеем регулярную точку данной ветви. Точки диаграммы стационарных решений, в которых пара комплексно-сопряженных собственных чисел пересекает мнимую ось, называются точками комплексной бифуркации1) или точками бифуркации Хопфа, по имени математика, опубликовавшего одну из основополагающих работ о характере решений в окрестности таких точек. Следующий существенный факт мотивирует разработку алгоритмов для нахождения точек комплексной бифуркации: в указанных точках ( при выполнении определенных условий) от ветви стационарных решений отходит ветвь периодических решений. [12]
При параметрическом исследовании выбранной задачи нас обычно интересуют все ветви на диаграмме стационарных решений. Критические точки диаграммы стационарных решений характеризуются тем, что одно из собственных чисел матрицы Якоби для правых частей исходных дифференциальных уравнений равняется нулю. [13]
Страницы: 1