Абсцисса - вершина
Cтраница 1
 |
Построение регулировочной характеристики с помощью характеристического треугольника. [1] |
Абсцисса вершины А дает искомое значение тока возбуждения. Доказательство справедливости этого положения дано при построении внешней характеристики. [2]
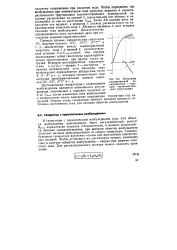
 |
Принципиальная схема генератора с параллельным возбуждением ( а и зависимости изменения ЭДС и падения напряжения в цепи возбуждения iB 1 /. B при изменении тока возбуждения генератора ( б. [3] |
Абсцисса вершины А дает искомую величину тока возбуждения. Доказательство справедливости этого построения приведено при построении внешней характеристики. Эти отрезки представляют собой гипотенузы характеристических треугольников при различных токах нагрузки. Искомая регулировочная характеристика / / ( /) - кривая 3 - построена в нижнем координатном углу. [4]
Абсцисса вершины кривой соответствует оптимальной температуре при данной степени превращения. [5]
Абсцисса вершины графика трехчлена f ( y) y2 - 4у - а равна 2, так что если трехчлен имеет корни, то больший корень больше 2 и он нас не интересует. Поэтому остается написать условие, при котором на интервале 0 у 1 имеется ровно один корень. [6]
Абсцисса вершины графика трехчлена f ( y) y2 - 4у - а равна 2, так что если трехчлен имеет корни, то больший корень больше 2 и он нас не интересует. Поэтому остается написать условие, при кото - Ром на интервале 0 у 1 имеется ровно один корень. [7]
Абсцисса вершины графика трехчлена f ( y) - y2 - 4z / - а равна 2, так что если трехчлен имеет корни, то больший корень больше 2 и он нас не интере сует. Поэтому остается написать условие, при котором в промежутке 0 у 1 имеется ровно один корень. [8]
А Абсцисса вершины данной параболы равна ( а - 1) / 2 и на интервале ] - оо; ( а - 1) / 2 [ данная функция возрастает. [9]
Так как абсцисса вершины параболы оказывается внутри интервала - 1 г 1, а сама парабола направлена рогами вверх, то условие задачи равносильно тому, что ордината вершины положительна. [10]
Обозначим через цц абсциссы вершин шероховатостей. Возвышения неровностей второй поверхности в начальный момент времени будем отсчитывать от некоторой прямой, проведенной на расстоянии А0 от оси абсцисс и жестко связанной: со второй поверхностью, так что величина h Й0 ( 1 - е) будет текущим абсолютным расстоянием между поверхностями. Начало отсчета совместим с началом участка длины L, и пусть L будет одинаково для обеих поверхностей. [11]
Какое значение должна иметь абсцисса вершины /), чтобы площадь прямоугольника ABCD была наибольшей. [12]
Тогда D 0, так как кор ни действительны, абсцисса вершины - Ь / ( 2а большее. О, так как d лежит вне интервала между корнями. Обрат но, пусть выполнены указанные три условия. [13]
Знак Ь определяется из формулы х - -, где х0 - абсцисса вершины параболы. [14]
Мы видим, таким образом, что показательный множитель не только уменьшает амплитуды колебаний, но и смещает абсциссы вершин кривой. [15]
Страницы: 1 2