Ашкенази
Cтраница 1
Ашкенази и Хеллер [9] установили, что реакция между этиленом и хлором идет в присутствии свинца как катализатора; температуру реакционной зоны следует при этом поддерживать ниже 100 С. [1]
Ашкенази было отмечено, что в то время как температура воспламенения чистого бензола равняется 662 С, таковая для обычного ( бензола не превышает 570 С вследствие разложения присутствующих в нем тиофенов. [2]
Как отмечалось Ашкенази и Поздняковым [11], испытания образцов, представленных схематически на рис. 8, а, связаны с двумя трудностями: 1) преждевременным разрушением из-за нагружения матрицы у концов волокон сдвигающими напряжениями; 2) сложностью получения однородного напряженного состояния. Применение широких образцов смягчает первую из перечисленных трудностей, но усугубляет вторую, так как для получения приблизительно однородного напряженного состояния одноосного растяжения отношение длины образца к ширине должно быть не менее трех. [4]
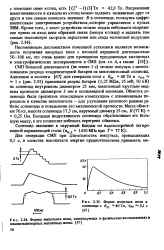 |
Форма импульса поля в соленоиде с Вт 40 Тл, Т00 0 1 с.| Формы импульсов поля, используемых в физических исследованиях в квазистационарных магнитных полях. [5] |
Ашкенази и коллеги [67] для генерации поля с Вт 40 Тл и TOO 1 с ( рис. 2.35) применили разряд батареи ( 1 25 МДж, 25 мФ, 10 кВ) на соленоид внутренним диаметром 25 мм, намотанный круглым медным проводом диаметром 3 мм в полиамидной изоляции. Обмотка соленоида была пропитана эпоксидным компаундом с алюминиевым порошком в качестве наполнителя - для улучшения теплового режима работы соленоида и повышения его механической прочности. [6]
Концентрация кислорода и давление оказывают значительное влияние на температуру самовоспламенения, и не существует еще закона, позволяющего заменять одно другим. В частности, укажем на очень интересные исследования этого вопроса, произведенное Ашкенази в Химическом институте в Карлсруэ в части определения пределов воспламенения, происходящих под давлением. [7]
Как указывалось, прочность изделия при сложном напряженном состоянии может быть определена при помощи одного из критериев прочности. Проведенный анализ наиболее широко распространенных критериев прочности для композиционных анизотропных материалов показал, что в наибольшей степени удовлетворяют этим требованиям критерии прочности Мизеса - Хилла, Фишера, Прагера, Веррена, Норриса, Ашкенази. [8]
Поверхности прочности различных анизотропных композитов соответствуют многочисленным механизмам разрушения и могут иметь самые разнообразные размеры и форму, так что для описания таких поверхностей необходимо иметь достаточно гибкую математическую модель. Несмотря на то что форма поверхности прочности может быть достаточно сложной, по аналогии с выводами общей теории пластичности можно ожидать, что она будет выпуклой ( Поль [38]), но даже при отсутствии выпуклости ( Ашкенази [1]) для любой заданной траектории на-гружения условие разрушения, записываемое в виде некоторого уравнения, имеет только один корень. Например, две прямолинейные траектории, идущие вдоль коллинеарных лучей, пересекают, как показано на рис. 2 а, поверхность прочности не более чем в двух точках. Наличие единственного корня ( рис. 2 6), означающее, что для некоторых траекторий нагружения материал обладает бесконечной прочностью, физически допустимо, но в инженерной практике встречается редко. [9]
Константы ап и аы для & в уравнении ( 67) можно найти по формулам ( 666), измеряя пределы прочности в экспериментах с образцами, вырезанными из материала под разными углами 6 и 6; следовательно, в уравнения ( 67) входит 30 неизвестных постоянных, соответствующих индексам k ф I. Выход из этого положения, предложенный Ашкенази, состоит в определении шести постоянных для k I 1, 2, 3 при дополнительном произвольном предположении о том, что остальные 24 постоянных равны нулю. [10]
Страницы: 1
