Масштаб - скорость
Cтраница 2
Для графического решения выбираем масштаб скорости и проводим вектор - vn в масштабе. Затем через точку А проводим вертикаль и, отложив угол 40, проводим линию АВ. Измерив полученные векторы и умножив на масштаб, получим относительную и абсолютную скорости. [16]
Для графического решения выбираем масштаб скорости и проводим вектор - е в масштабе. Затем через точку А проводим вертикаль и, отложив угол 40, проводим линию АВ. Измерив полученные векторы и умножив на масштаб, получим относительную и абсолютную скорости. [17]
Так как ц - масштаб скорости и у-i - масштаб чертежа есть величины постоянные, то угловые скорости oi и шз прямо пропорциональны тангенсам углов pi и ра. [18]
В принципе в качестве масштаба скорости турбулентного движения аоиет быть принята любая потерянная скорость V - ц) в пределах данного потока; при этом между бавовым масштабом скор - ста к приня-тнм масштабом всегда имеет место однозначная связь. [19]
Тш / а и масштабом скорости vt, а поток в целом может быть автомодельным, если те же самые масштабы являются подходящими для автомодельного развития внешнего потока. [20]
Мв, М - - масштабы скорости и ускорения, одинаковые для любой пары сходственных точек. Скорости и ускорения должны быть представлены одинаково ориентированными в пространстве векторами. [21]
Тр представляет собой по существу масштаб скорости пульсационного движения частиц. [22]
Из этих точек откладывают в масштабе скоростей отрезки, соответствующие локальным скоростям в точках замера. [23]
 |
Четырехшарнирный механизм с планами скоростей и ускорений. [24] |
Для построения плана скоростей необходимо установить масштаб скорости. [25]
Используя зависимость (VII.18), следует учитывать масштаб скоростей. [26]
Выбор постоянной k влияет только на масштаб скоростей и поэтому не имеет значения. [27]
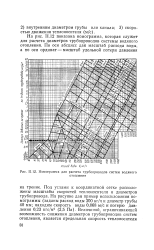 |
Номограмма для расчета трубопроводов систем водяного. [28] |
Под углами к координатной сетке расположены масштабы скоростей теплоносителя и диаметров трубопровода. [29]
По-разному складывается также ситуация в отношении масштаба скоростей. Если рассматривается конвекция при вынужденном движении среды ( вынужденная конвекция), то подразумевается, что уровень скоростей задан условиями задачи. Следовательно, в этом случае всегда может быть выбран естественный масштаб скоростей, и зависимые переменные wx, wy, w, будут простыми отношениями - симплексами. Одновременно ( и это чрезвычайно важно) из динамического уравнения движения должен быть опущен член pg, выражающий действие силы тяжести. В результате из безразмерных комплексов ( 4 - 35) и ( 4 - 36) выпадает число Фруда. [30]
Страницы: 1 2 3 4