Идеально пластичный материал

Cтраница 1

Идеально пластичный материал характеризуется зависимостью сил сопротивления только от скорости деформации, работа деформации полностью поглощается материалом. [1]

Плоское напряженное состояние. [2]

Для идеально пластичного материала К - 2, а для идеально хрупкого К - I. В первом случае прочность материала определяется только касательными напряжениями, а во втором - только нормальными напряжениями. [3]

Рассмотрим вначале случай идеально пластичного материала. [4]

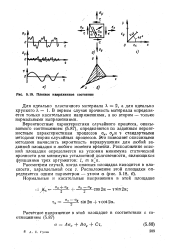
Наиболее простой является диаграмма идеально пластичного материала ( фиг. [5]

Приложение к образцу из идеально пластичного материала растягивающей силы Ps - Fas ( F - площадь сечения образца) вызывает неограниченный рост его деформаций или текучесть. Напряжений, больших чем предел текучести os, в таком материале возникнуть не может. [6]

Переход от чисто упругого состояния равновесия к состоянию равновесия идеально пластичного материала может быть изучен на цилиндрическом или призматическом стержне постоянного поперечного сечения, подвергнутом кручению относительно его оси и деформированию за пределом текучести. Хотя излагаемые4 в этой главе методы исследования поля напряжений, отвечающего таким условиям, и опираются скорее на визуальные, чем на аналитические средства, они все же дают возможность получить основные уравнения, характеризующие это поле. [7]

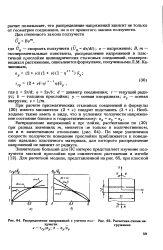Распределение напряжений с учетом под - [ IMAGE ] Расчетная схема на-зучести. гружения. [8]

По мере увеличения скорости ползучести поведение прослойки приближается к поведению идеально пластичного материала, для которого распределение напряжений не зависит от радиуса. [9]

Теоретически можно показать, что быстрое разрушение в сосуде, выполненном из идеально пластичного материала и работающем при температуре ниже интервала ползучести, может наступить только при определенных, довольно сложных системах на-гружения. Эдмунс и Бир [86] для бруса прямоугольного сечения, нагруженного циклическим изгибающим моментом и циклической осевой силой, показали, что быстрое разрушение не наступает, если в зоне нейтральной оси бруса не повторяется циклически пластическое деформирование. Бир [87] показал также, что подобный критерий применим для случая повторного термического напряжения и циклической осевой силы. По аналогии соответствующие условия применительно к сосудам должны заключаться в том, чтобы в средней зоне по толщине стенки не было повторного циклически пластического деформирования. [10]

Если зс at с0, поверхность становится круговым цилиндром, и из уравнения (15.20) мы вновь получаем зависимость (15.17), представляющую условие токт const течения идеально пластичного материала. [11]

Два предельных случая т1, & 2 и т 0, &1, очевидно, соответствуют чисто вязкому материалу ( при коэффициенте вязкости ( i const) и идеально пластичному материалу, течение которого происходит при постоянном пределе текучести токт 0 2 / 3) а0 const, где ао - предел текучести при растяжении. На рис. 16.40 показано распределение радиального, и тангенциального напряжений около кругового отверстия при установившейся ползучести бесконечной пластины. [12]

Распределение напряжений в нихроме ( /. [13]

Расчеты выполнены для композиции с объемным наполнением /, равным 15 % при условии, что нихром испытывает пластическую деформацию, если напряжения в нем превысят предел текучести и он ведет себя как идеально пластичный материал. [14]

Идеально упругий материал дает бесконечно быстро возникающую иод действием внешней силы деформацию, которая однозначно определяется величиной вызвавшей ее силы. Идеально хрупкий материал под действием внешней силы сначала дает только упругую деформацию, а после достижения предела упругости его сплошность разрушается. Идеально пластичный материал не имеет упругости и при постепенном увеличении нагрузки сначала не изменяет формы, а когда нагрузка достигает предела текучести, возникает непрерывная деформация без разрыва сплошности. Форма, приобретенная в момент снятия нагрузки, полностью сохраняется; релаксация внутренних напряжений бесконечно быстрая, и упругого последействия нет. [15]

Страницы: 1 2