Циклически упрочняющийся материал

Cтраница 3

Основные закономерности, описывающие кинетику циклической и односторонне накапливаемой деформаций основаны на принципе обобщенной диаграммы циклического деформирования, а их форма в виде уравнений (2.10) и (2.18) относится к случаю симметричного нагружения. Если для циклически упрочняющихся материалов этот эффект выражен незначительно и в первом приближении для оценки кинетики деформаций могут быть использованы лишь амплитудные значения действующих напряжений и деформаций, то для циклически стабильных, а тем более разупрочняющихся материалов существенное значение имеют и средние напряжения цикла. [31]

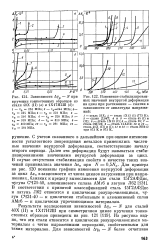
Таким образом, анализируя рассмотренные выше экспериментальные данные по малоцикловому деформированию при мягком режиме нагружения с временными выдержками на экстремумах нагрузки ( см. рис. 4.8 - 4.10), можно видеть, что как температура испытаний, так и форма цикла накладывают свои особенности на кинетику деформаций в этих условиях. Причем для циклически упрочняющихся материалов в двойных логарифмических координатах, что соответствует степенному виду кинетической функции, они представляют собой прямые ниспадающие линии ( рис. 2.3, б), а для циклически разупрочняющихся материалов в полулогарифмических координатах - прямые восходящие линии ( рис. 2.3, а), отвечающие экспоненциальному виду этих зависимостей. Как показывают приведенные выше экспериментальные данные для высоких температур и сложной формы цикла нагружения, в этих условиях наблюдается более сложный характер поведения деформационных характеристик. Так, уже при 450 С сталь Х18Н10Т обнаруживает в исходных циклах некоторое упрочнение, переходящее затем на основной стадии процесса деформирования в циклическое разупрочнение, причем это характерно как для нагружения с треугольной, так и с трапецеидальной формами цикла. Если при t - 450 С степень разупрочнения еще невелика, то с повышением температуры до 650 С, когда начинается интенсивное проявление в материале темпера-турно-временных эффектов, кинетика деформаций становится ярко выраженной и в существенной степени зависящей от времени, формы цикла и уровня нагружения. Указанные обстоятельства не учитываются зависимостями (2.10), (2.18) и для их описания было предложено [13] связать параметры этих уравнений с механическими свойствами материалов, а последние рассматривать зависящими от температуры и времени нагружения. [32]

На-основе этих моделей представляется возможным аналитически описать форму петли упруго-пластического гистерезиса, эффект Баушингера, а также процесс изменения напряжений и деформаций. Применительно к циклически упрочняющимся материалам Ю. Д. Соф-роновым получена зависимость между напряжениями, деформациями и числом циклов до разрушения. [33]

Наблюдают также отклонение от линейной зависимости ( 5) параметров а и р при высоких уровнях нагружения. Например, у циклически упрочняющегося материала В-96 параметр а при деформациях е ( 0 Щ, проходя через максимум, уменьшается. [34]

Кинетика изменения максимальных напряжений зависит от свойств материала и находится в соответствии с поведением различных групп материалов при мягком нагружении. Так, в испытаниях циклически упрочняющихся материалов при жестком нагружении амплитуда напряжения вначале возрастает. Интенсивность возрастания с увеличением числа циклов уменьшается. После сравнительно небольшого числа циклов амплитуда напряжений становится практически постоянной на большей части долговечности вплоть до разрушения. Размах установившегося напряжения иногда называют асимптотическим размахом или размахом насыщения. Предполагают, что каждому размаху деформации соответствует определенный асимптотический размах напряжения. [35]

Кинетика изменения максимальных напряжений зависит от свойств материала и находится в соответствии с поведением различных групп материалов при мягком нагружении. Так, в испытаниях циклически упрочняющихся материалов при жестком нагружении амплитуда напряжения вначале возрастает. Интенсивность возрастания с увели-чением числа циклов уменьшается. После сравнительно небольшого числа циклов амплитуда напряжений становится практически постоянной на большей части долговечности вплоть до разрушения. Размах установившегося напряжения иногда называют асимптотическим размахом или размахом насыщения. Предполагают, что каждому размаху деформации соответствует определенный асимптотический размах напряжения. [36]

Определение малооикловой дач го-вечности осуществляется по экспериментальным или расчетным кривым малоциклового разрушения - уравнения на с. Эти кривые для циклически стабильных и циклически упрочняющихся материалов строят для жесткого ( по заданным деформациям) нагружения, а для анхлическн авн-зотролаых разупрочняющихся материалов - для жесткого я мягкого ( по заданным напряжениям) нагружений. [37]

Кривая k 1 - это кривая деформирования, получаемая при обычном статическом испытании образца. Семейство кривых, расположенных выше указанной кривой, соответствует циклически упрочняющемуся материалу, а семейство кривых, расположенных ниже - циклически - разупрочняющемуся материалу. Видно, что упрочняющийся материал в процессе циклического деформирования приобретает свойства, приближающие его к упругому материалу, а разупрочняющийся - к идеально пластическому. [38]

Исследования циклического упругопластического деформирования показали, что после определенного числа циклов у циклически упрочняющихся материалов ( а иногда и у циклически раз упрочняющихся) наступает стационарное состояние, при котором в последующих циклах повторяются соответствующие диаграммы деформирования. Схема, приведенная на риса 99, я, характерна для циклически упрочняющихся материалов, когда ширина петли с числом полуциклов уменьшается. Деформация, накопленная в процессе циклического деформирования, стремится в этом случае к некоторой предельной величине, которая ос тается постоянной вплоть до образования трещины, после чего возможно некоторое увеличение. Схема, приведенная на рис. 99, б, характерна для циклически стабильных материалов, когда ширина петли в - каждом полу цикле остается неизменной. [39]

Так как с повышением предела текучести уменьшается доля пластической составляющей при заданной стесненной деформации, то можно выявить общую закономерность сопротивления материалов термической усталости. В области малых чисел циклов до разрушения ( при большой величине стесненной деформации за цикл) преимущество имеют высокопластичные циклически упрочняющиеся материалы, а в области больших долговечностей ( при малой величине стесненной деформации за цикл) - высокопрочные материалы. Во всем практически важном для теплоэнергетического оборудования диапазоне температур преимущество должны иметь высокопластичные материалы. Указанная закономерность хорошо подтверждается многочисленными экспериментальными данными. [40]

Образцы для испытаний на.| Гладкие образцы для испытаний на малоцикловую усталость. [41]

С связан с пластичностью при разрушении, вызванном статическим растяжением. При циклическом нагружении с заданным размахом напряжения ( см. рис. 6, б) р процессе испытания сохраняются постоянными значения 0тах и own, ширина же петли гистерезиса от цикла к циклу может изменяться в зависимости от особенностей материала: уменьшаться для циклически упрочняющихся материалов, увеличиваться - для циклически раз-упрочняющихся материалов и, наконец, сохраняться неизменной для циклически стабильных материалов. При этом процесс накопления пластических сдвигов может, рообще говоря, происходить вплоть до разрушения. [42]

Показано, что при мягком нагружении возможны три различных случая накопления суммарной пластической деформации в зависимости от числа полуциклов. Характеристикой величины пластической деформации при циклическом нагружении служит ширина петли деформирования за полуцикл. Для циклически упрочняющихся материалов остаточная деформация за полуцикл уменьшается с числом циклов и стремится к некоторой постоянной предельной величине; для циклически разупрочняющихся материалов ширина петли и суммарная деформация увеличиваются с числом циклов; для циклически стабильных материалов ширина петли гистерезиса, начиная с некоторого полуцикла, становится постоянной и не зависит от числа циклов. [43]

Приведенные примеры показывают, что уравнения (2.6.4), (2.6.5) позволяют достаточно точно описать кинетику изменения напряжений и деформаций при разнообразных программах нагру-жения. Отметим, однако, что удовлетворительные результаты получаются при программах нагружения, включающих циклы с различными амплитудами напряжений при отсутствии среднего напряжения в цикле. Использование уравнений для расчета диаграмм деформирования асимметричных циклов дает эффект одностороннего накопления пластических деформаций, что не наблюдается в экспериментах для циклически упрочняющихся материалов. [44]

Зависимости Дун - N при.| Изменение стабилизированных значений неупругой деформации на цикл при растяжении - сжатии в зависимости от амплитуды напряжений. [45]

Страницы: 1 2 3 4