Матрица - реакция
Cтраница 1
Матрицы реакций и соответствующие векторы реакций для треугольного конечного элемента вычисляются в глобальной системе координат пластинчатой системы Ох и в дальнейшем их преобразовании при формировании разрешающей системы уравнений нет необходимости. [1]
Соответственно матрица реакции представляет собой не какую-либо отдельную реакцию, а целую категорию с общим законом перераспределения электронов, называемую Л - категорией. Таким образом, Л - категория представляет собой класс эквивалентных реакций с одинаковым законом переопределения электронов и одинаковым размещением участвующих связей. За некоторым исключением основные химические реакции в органической химии протекают при перераспределении электронов между атомами от одного до шести. [2]
 |
Блок-схема расчета надземного бескомпенсаторного перехода. [3] |
Здесь вычисляется матрица реакций ( грузовых членов) от поперечной нагрузки, воздействия температуры и внутреннего давления с учетом продольно-поперечного изгиба элемента. Последний фактор обусловил наличие таких же, как в блоке 2, трех подблоков. [4]
Очевидно, матрица реакций, полученная в результате преобразований, симметрична. [5]
Для построения матрицы реакций в глобальной нумерации ( для узлов 1 к 2, см. рис. 8.5, а) из матрицы ( 9 57) используется только блок гьк. [6]
С помощью матрицы реакции рассчитывается f - функция Ландау и определяются коэффициенты ее разложения по полиномам Лежан-драа В результате получено очень хорошее согласие расчетных и экспериментальных данных. [7]
Если в матрице реакции поменять два столбца и две строки местами ( например, С и В), не меняя меток, то будут получены другие продукты реакции, однако матрица реакции будет принадлежать той же категории. В данном примере N не может быть более четырех, поскольку число возможных связей равно двум. [8]
Наличие в матрице реакций нулевых строк и столбцов необходимо учитывать при численной реализации алгоритма расчета на ЭВМ. Так, если все пластинки, соединенные с каким-либо узлом, лежат в одной плоскости, в СЛАУ появляется уравнение вида 0 0, поэтому введем фиктивный коэффициент жесткости, равный единице. В результате угол хг поворота этого узла оказывается равным нулю. [9]
Дальнейший алгоритм построения матрицы реакций аналогичен приведенному в начале данного параграфа. [10]
Дальнейший ход построения матрицы реакций аналогичен приведенному в начале параграфа. [11]
Рассмотрим процесс построения матрицы реакций на примере четырехугольника, изображенного на рис. 11.34, в; для остальных случаев построения аналогичны. [12]
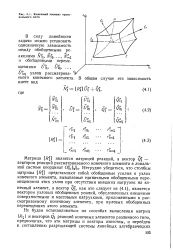 |
Конечный элемент произ - / г. [13] |
Матрица [7. ] является матрицей реакций, а вектор Qf - вектором реакций рассматриваемого конечного элемента в локальной системе координат О з - Нетрудно убедиться, что столбцы мдтрицы [ R ] представляют собой обобщенные усилия в узлах конечного элемента, вызываемые единичными обобщенными перемещениями этих узлов при отсутствии внешних нагрузок на конечный элемент, а вектор Q, как это следует из (4.1), является вектором узловых обобщенных усилий, обусловленных внешними поверхностными и массовыми нагрузками, приложенными к рассматриваемому конечному элементу, при нулевых обобщенных перемещениях этого элемента. [14]
Матрица г является матрицей реакций в глобальной системе координат. Для перевода в глобальную систему используют матрицы направляющих косинусов. [15]
Страницы: 1 2 3 4