Матрица - система
Cтраница 3
Матрица системы ( 5) для случая JV5 условно изображена на рис. 15, где крестиками отмечены ненулевые элементы. [31]
Матрица системы Л и ее правая часть / во многих случаях задаются приближенно. Причины погрешности могут быть самые разные - от ошибок округления при вводе чисел в машину до ошибок измерения, если система связана с обработкой экспериментальных данных. [32]
Матрица системы (4.14) имеет треугольный вид. На этом заканчивается прямой ход метода Гау сса. [33]
Матрица системы (4.53) вырожденная, поскольку ее определитель (4.48) равен нулю. [34]
Матрицы систем (8.107) и (8.108) трехдиагональные, и для решения этих систем может быть использован метод прогонки. [35]
Матрица системы является трехдиагональной и симметричной. [36]
Матрица системы имеет верхнетреугольную форму. [37]
Матрица системы линейных уравнений (3.3.10) имеет трехдиаго-нальную структуру, и поиск решения не вызывает затруднений. После окончания вычислений может быть оценена степень ухудшения качества модели из-за перехода к описанию регрессионного уравнения непрерывной ломаной. Для этого нужно сопоставить значения критерия, вычисленные по формулам (3.3.6) и (3.3.9) для оптимальных кусочно-линейных моделей. [38]
Матрицу системы преобразуют к треугольному виду, после чего решение получают обратной прогонкой. [39]
Матрицей системы линейных уравнений (6.16) называется прямоугольная таблица, составленная из коэффициентов при неизвестных в системе ограничений. [40]
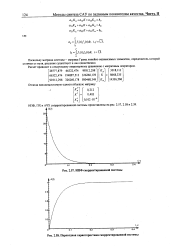 |
ИПФ скорректированной системы.| Переходная характеристика скорректированной системы. [41] |
Поскольку матрица системы - матрица Грама линейно независимых элементов, определитель которой отличен от нуля, решение существует и оно единственно. [42]
Поскольку матрица системы (9.6) является треугольной, то для решения этой системы на компьютере путем последовательного определения ут требуется меньший объем вычислений и, соответственно, значение N можно выбрать значительно большим, чем в случае уравнения Фредгольма. [43]
Гамильтонова матрица системы совпадает с полученной при решении задачи 6.1 ( в базисе г, - г) с точностью до замены цВа на А. [44]
Пусть матрица системы имеет группу больших сингулярных чисел, а остальные сингулярные числа соизмеримы с точностью входных данных или меньше. [45]
Страницы: 1 2 3 4