Матур

Cтраница 1

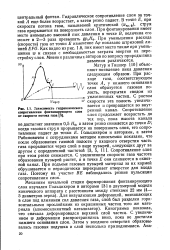Зависимость гидравлического Ва6ТСЯ и превращается во внут-сопротивления фонтанирующего слоя реннии канал. Сопротивление от скорости потока газа [ б ]. слоя продолжает возрастать до. [1]

Матур и Гишлер [10] объясняют появление пика давления следующим образом. При расходе газа, соответствующем точке А, у нижнего основания слоя образуется газовая полость, перекрытая сводом из уплотненных частиц. [2]

Ар матура трубопроводная общего назначения. [3]

Первоначально Матуром и Гишлером [137] было показано, что градиент давления в кольце на любой высоте зависит от скорости поднимающегося через кольцо газа WK на этой высоте. [4]

Первый метод применяли Матур и Торли с сотрудниками [137, 227, 228], которые экспериментально определили соотношение между скоростью газа и перепадом давления для неподвижного свободно засыпанного ( рыхлого) слоя. [5]

Нк, полученные Матуром и Гишлером [137, 138] для колонн диаметром 15 2 и 30 5 см, в то время как значения, рассчитанные по уравнению (6.5) [129], получены для аппарата диаметром 61 см. Отсутствие согласия с данными Мамуро и Хаттори ( показанное также на рис. 3.4), вероятно, не удивительно, если принять во внимание уже обсуждавшиеся трудности при определении скоростей воздуха в кольце с помощью трубки Пито. [6]

Такое уменьшение эффективности наблюдали также Матур и Гишлер [139] в опытах с системой жидкость - твердое, при фонтанировании известняка разбавленной соляной кислотой. [7]

Для средней части слоя Бридгватером и Матуром [30] предложена модель равновесия сил, учитывающая соударения твердых частиц и основанная на принципах воронкообразного течения твердых частиц. Верхняя часть слоя из рассмотрения исключается, поскольку принимается, что соударения твердых частиц должны быть независимыми от высоты слоя - допущение, основанное на поведении твердых частиц при воронкообразном течении и, справедливое только при достаточно большой высоте фонтанирующего слоя. [8]

Следует, однако, указать, что Матур с сотрудниками [137, 227, 228] в ранней работе измерили скорость частиц по киносъемке без учета радиальных колебаний. Поскольку скорость измерялась на определенном уровне слоя, то следовательно, она лишь приблизительно отвечала среднему радиальному значению, из которого с помощью описанных выше методов вычисляется средний радиальный профиль порозности. [9]

В заключение следует отметить, что модель, предложенная Матуром и Лимом [144], дает возможность проанализировать не только химическую реакцию, но также и процессы тепло-и массообмена в фонтанирующих слоях. Их двухзонная модель, несмотря на ее необоснованность, представлена здесь полностью в надежде, что она будет стимулировать дальнейшие исследования фонтанирования во всех трех направлениях. [10]

Эти уравнения получены Беккером на основе собственных данных, а также результатов Матура и Гишлера. Что касается точности, то сам Беккер не дает никаких указаний, насколько вычисленные значения и. Впоследствии такое сравнение проведено Манурунгом [134], который использовал экспериментальные данные для целого ряда различных материалов, полученные в аппаратах диаметром только 15 см. Манурунг отметил, что влияние увеличения высоты слоя несколько переоценивается в уравнении - (2.38) и недооценивается в уравнении Беккера, однако четко не установил, которое же из двух уравнений более приемлемо. Поэтому, вероятно, для аппаратов малых диаметров нет особого смысла использовать относительно сложное уравнение Беккера. [11]

Стил и Тодос [22-24] подробно исследовали эту корреляцию для неполярных и полярных газов, Флинн и Тодос [25] - для углеводородов, Матур и Тодос [26] - для высокотемпературных газов, диссоциированных и недиссоциированных. [12]

Это соотношение приводит к тем же результатам для величин с. Финдли и Матур определяют типичную область изменения величин ос / тс. [13]

Чтобы сравнить фонтанирующий слой с другими системами для выполнения реакций, необходимо иметь возможность предсказывать степень конверсии для-реактора. Имея это в виду, Матур и Лим [144] использовали предложенный ранее Емаки [234] подход и выдвинули теоретическую модель реактора с фонтанирующим слоем, в том числе и для реакции в паровой фазе в присутствии катализатора или частиц теплоносителя. Теория позволяет рассчитать степень превращения химической реакции в общем виде, но ценность ее снижается тем, что она не дает полной информации о гидродинамической характеристике фонтанирования. Однако теоретическая модель приведена в такой форме, что полученную информацию можно легко систематизировать. [14]

Галецкий [4], впервые изучавший действие рентгеновских лучей на коллоидные растворы золота, установил, что при облучении изменяется их стабильность. Позднее, Батагар, Гупта, Матур [5] установили, что при действии рентгеновских лучей на золи золота, серебра, меди, гидроокиси железа и гидроокиси меди, золи, защищенные органическими веществами, не теряют стабильности, тогда как те же золи, в отсутствии органических веществ, но при достаточно высоком содержании электролитов претерпевают существенные изменения при продолжительном облучении. [15]

Страницы: 1 2