Машина - больцман
Cтраница 1
Машина Больцмана была предложена и исследовалась во второй половине 1980 - х годов. [1]
Машины Больцмана обладают хорошими способностями к обучению. Машина научилась также делить предложения на отдельные слова и даже понимать простые предложения. [2]
Свойства машины Больцмана широко изучались. В работе [1] показано, что скорость уменьшения температуры должна быть обратно пропорциональна логарифму времени, чтобы была достигнута сходимость к глобальному минимуму. [3]
Принцип машины Больцмана может быть перенесен на сети практически любой конфигурации, хотя устойчивость не гарантируется. Для этого достаточно выбрать одно множество нейронов в качестве входов и другое множество в качестве выходов. [4]
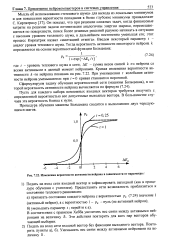 |
Изменения вероятности активности нейрона в зависимости от параметра t. [5] |
Процедура обучения машины Больцмана сводится к выполнению двух чередующихся шагов. [6]
Пусть цель обучения машины Больцмана состоит в построении внутренней модели, воспроизводящей вероятностную взаимосвязь между структурами двух классов. [7]
Развитием модели Хопфилда является машина Больцмана, предложенная и исследованная Дж. [8]
Перейдем теперь к описанию процедуры, посредством которой производится обучение машины Больцмана. [9]
Известны четыре основных типа правил обучения: коррекция по ошибке, машина Больцмана, правило Хебба и обучение методом соревнования. [10]
Несмотря на улучшение скорости обучения, даваемое машиной Коши по сравнению с машиной Больцмана, время сходимости все еще может в 100 раз превышать время для алгоритма обратного распространения. Отметим, что сетевой паралич особенно опасен для алгоритма обучения Коши, в особенности для сети с нелинейностью типа логистической функции. Бесконечная дисперсия распределения Коши приводит к изменениям весов неограниченной величины. Далее, большие изменения весов будут иногда приниматься даже в тех случаях, когда они неблагоприятны, часто приводя к сильному насыщению сетевых нейронов с вытекающим отсюда риском паралича. [11]
В то же время многие нейронные парадигмы, такие как сети Кохонена или машина Больцмана не имеют прямых аналогов среди статистических методов. [12]
 |
Распределение Коши и распределение Больцмана. [13] |
Этот вывод подтвердился экспериментально. Машины Больцмана часто требуют для обучения очень большого ресурса времени. [14]
Тогда процедура обучения машины Больцмана выглядит особенно просто. [15]
Страницы: 1 2