Электронная цифровая машина
Cтраница 2
Кроме электронных цифровых машин, которые применяются для решения различных сложных математических проблем физики и техники, существует группа моделирующих машин, используемых для управления производственными процессами, а также в тех случаях, когда необходимо быстро решить поставленную задачу. [16]
Возможности электронных цифровых машин в значительной степени определяются тем, на каких элементах строятся эти машины. [17]
Применение электронных цифровых машин позволяет автоматизировать расчеты на прочность типовых и сложных конструкций. [18]
Элементы электронных цифровых машин, реализующие основные логические функции НЕ, И, ИЛИ, называются основными логическими элементами. [20]
Применение электронных цифровых машин при нахождении оптимальных решений в деревообрабатывающей промышленности Польши. [21]
Применение электронных цифровых машин для учстно-вычислительных операций позволит производить последние значительно быстрее, выполнять более сложные операции и гибко изменять программу операций. [22]
Большинство электронных цифровых машин имеют несколько различных видов запоминающих устройств. [23]
У больших электронных цифровых машин блоки скомпонованы в специальных стойках или шкафах по функциональным признакам. [24]
Для электронных цифровых машин малой и средней мощности язык АЛГОЛ-60 является чересчур сложным, чтобы организовать эффективный перевод с него на язык машины. [25]
Применяя электронную цифровую машину для решения математических задач, необходимо учитывать ее особенности как вычислительного инструмента. [26]
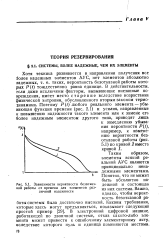 |
Зависимости вероятности безотказной работы от времени для элементов различной надежности. [27] |
В электронной цифровой машине, работающей по двоичной системе, отказ какого-либо элемента может привести к ошибочному элементарному акту, вследствие которого нуль и единица поменяются местами. [28]
 |
Логическая схема двоичного полусумматора. [29] |
В электронной цифровой машине наличию или отсутствию события соответствует наличие или отсутствие электрического сигнала, а выполнение логических операций достигается с помощью трех основных логических схем: 1) собирательной схемы ( логическая схема ИЛИ), дающей на выходе сигнал при наличии одного ИЛИ нескольких сигналов на входах; 2) схемы совпадений ( логическая схема И), дающей сигнал на выходе при одновременном наличии сигналов на всех входах; 3) схемы отрицания ( логическая схема НЕ), дающей сигнал на выходе при отсутствии сигнала на входе. [30]
Страницы: 1 2 3 4
