Банна

Cтраница 1

Банна, С. Н. Журкова, Ю. С. Лазуркина, Г. Л. Слонимского и других исследователей) сформировались современные представления о строении высокомолекулярных соединений. [1]

Банна, С. Н. Журкова, Ю. С. Ла-зуркина, Г. Л. Слонимского и других исследователей) сформировались современные представления о строении высокомолекулярных соединений. [2]

Схема секториального строения кристалла типа структуры песочных часов. [3]

Банна, Руайе и других авторов, Бакди рассматривает как второстепенный. [4]

Банна, С. Н. Журко-за, Ю. С. Лазуркина, Г. Л. Слонимского и других исследователей) сформировались современные представления о строении высокомолекулярных соединений. [5]

Согласно Банну [63], неориентированный полимер представляет собой смесь кристаллических и некристаллических областей, равномерно распределенных в полимере. Одна и та же цепная молекула может проходить через несколько кристаллитов, которые могут оказывать влияние друг на друга. В последующей работе Банна [26] было выдвинуто представление о неориентированном кристаллическом полимере как о сферолитном образовании. Отдельные сферолиты представляют собой скопление кристаллитов с радиально-спиралевидной упаковкой. [6]

Согласно Банну [26], в процессе растяжения под влиянием механических сил кристаллиты извлекаются из сферолитных образований; каждый кристаллит вытягивает за собой другой вследствие их связи друг с другом через молекулу. При дальнейшем растяжении возможно разрушение кристаллитов, которое может в определенных случаях доходить до разделения на отдельные молекулы. Такое разрушение происходит в зоне шейки. После установления параллельного расположения кристаллитов или молекул они вновь объединяются в более крупные кристаллические образования. Если допустить, что разрушение кристаллов идет до их распада на отдельные молекулы, то можно сказать, что полимер, хотя и не во всей своей массе, но проходит через аморфное состояние, чему способствует также выделение тепла в зоне шейки. [7]

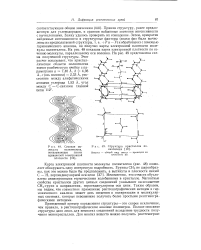Сечение молекулы полиэтилена, показывающее линии одинаковой электронной плотности.| Структура кристаллов полиэтилена. [8]

Приняв структуру, ранее предложенную для углеводородов, и сравнив найденные значения интенсивности с вычисленными, Банну удалось проверить их совпадение. [9]

Полиэтилентерефталат состоит из смеси кристаллических и аморфных участков, соотношение которых зависит от способа получения. В вытянутом волокне оси молекулярных цепей наклонены в отношении оси волокна так, что плоскость ( 230) остается вертикальной, а наклон ( 001) к оси волокна возрастает. Возникновение наклона, по мнению Даубени, Банна и Броуна [ 2031, связано с различным характером распределения молекулярных сил вокруг молекулярной оси в триклинном кристалле. [10]

Что это так и должно быть, почти самоочевидно, особенно если вспомнить, что в случае любого кристалла, растущего при диффузионном контроле, концентрация меняется вдоль любой грани очень сильно, причем самая высокая концентрация на углах и ребрах граней, а самая низкая - в центрах граней. И несмотря на неоднородность концентрации, грани обычно растут плоскими. Некоторые данные относительно величины изменения концентрации вдоль грани можно найти в работах Берга [ Berg, 1938 ], Банна [ Bunn, 19191 и Хэмфрис-Оуэна [ Humphreys-Owen, 1949a, б ], которые наблюдали концентрационные поля вокруг кристаллов, растущих из водных растворов, используя интерферометрическую технику. [11]

Доказательством того, что арабам было известно о совершен - иых и дружественных числах больше, нежели до сих пор предполагали, мы обязаны профессору Тунисского университета Мохам-меду Суисси, который недавно перевел и опубликовал [32] упоминавшееся ранее сочинение ибн аль - Баниы о совершенных н дружественных числах. Кроме того, группа советских историков из Средней Азии [38] обнаружила в рукописях Кутбэддина Ши-разн ( XIII в. Согласно их данным, числа 17296 и 18416 были известны как в Марокко ( аль - Банна), так и в Иране ( Кутбэддин) за три с половиной столетия до Ферма. Поэтому он ошибочно считает 2024 и 2296 второй парой дружественных чисел. Я указываю здесь на эту ошибку, так как в [38] она не была замечена. Далее, я хотел бы отметить, что более поздние исламские авторы не приводят никакого доказательства для излагаемого способа, в то время как Сабит написал свое теоретико-числовое сочинение, по образцу Начал Эвклида, совершенно строго и потратил на доказательства немало уснлвй. [12]

Страницы: 1