Название - алгоритм
Cтраница 1
Названия алгоритмов 301 - 417 ( так же как и названия алгоритмов из других изданий) даются здесь на английском языке. После них указывается местонахождение относящихся к ним материалов, причем первое из указаний относится к местонахождению самого алгоритма. [1]
Название алгоритма связано со способом расчета погрешностей в конкретных слоях. [2]
Далее следует название алгоритма и в скобках - список исходных данных ( аргументов) и результатов с указанием их типов. [3]
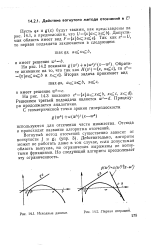 |
Исходные данные.| Первая итерация. [4] |
Отсюда и происходит название алгоритма отсечений. [5]
С этим связано и название алгоритма. [6]
Описанная форма БПФ носит название алгоритма Кули - Тьюки. [7]
Этот процесс известен под названием алгоритма Греффе. Он обобщается на случай многочленов более высокого порядка и комплексных корней. [8]
Внутри символа начала алгоритма записывают название алгоритма. Стрелка ведет к следующему символу. [9]
Внутри символа конца алгоритма записывают название алгоритма. [10]
Одна из форм преобразующей информации известна под названием алгоритмов. При этом под алгоритмом понимается система формальных правил или указаний, однозначно определяющая ход решения задачи и приводящая к правильному результату при любых значениях переменных. [11]
Используемый нами метод выделения признаков известен под названием алгоритма включения атрибутов. Включение атрибутов характеризует взаимосвязь между ними в той или иной выборке образов. В этом случае атрибут является синонимом дескриптора. [12]
Эта последовательность действий, описанная ниже, получает название алгоритма извлечения квадратного корня. [13]
Названия алгоритмов 301 - 417 ( так же как и названия алгоритмов из других изданий) даются здесь на английском языке. После них указывается местонахождение относящихся к ним материалов, причем первое из указаний относится к местонахождению самого алгоритма. [14]
Описанная процедура нахождения наибольшего общего делителя а и Ь носит название алгоритма Евклида; кольца, в которых эта процедура применима ( в частности - кольцо целых чисел или кольцо многочленов) иногда называют евклидовыми кольцами. [15]
Страницы: 1 2 3