Наклон - экспериментальная кривая
Cтраница 2
Для жидкостей, подчиняющихся полностью степенному закону течения, отпадает необходимость применения метода последовательных приближений, а коэффициент текучести п определяется по углу наклона экспериментальной кривой, нанесенной в логарифмических координатах. [16]
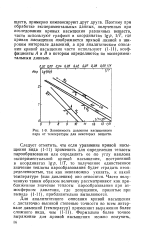 |
Зависимость давления насыщенного пара от температуры для некоторых веществ. [17] |
Следует отметить, что если уравнение кривой насыщения вида ( 1 - 11) применить для определения теплоты парообразования или определить ее по углу наклона экспериментальной кривой насыщения, построенной в координатах gp, l / T, то полученное единственное значение теплоты парообразования будет страдать неопределенностью, так как невозможно указать, к какой температуре ( или давлению) оно относится. Часто полученную таким образом величину рассматривают как приближенное значение теплоты парообразования при атмосферном давлении, где допущения, принятые при выводе ( 1 - 11), приблизительно выполняются. [18]
Соб и Сэт - теплоемкости образца и эталона); dT / dt - скорость изменения температуры нагревателя; RC ( fq / df - тангенс угла наклона экспериментальной кривой в любой точке, умноженный на постоянную Rco6 ( эта постоянная определяет разрешающую способность прибора); R - термическое сопротивление тепловому потоку. [19]
Тогда график зависимости 1 / т, от ( Atot - A) / A i позволяет найти отношение k - / а2 по точке пересечения с осью I / TJ, а отношение k - / л - по тангенсу угла наклона экспериментальной кривой. [20]
Необходимо обратить внимание на очень резкое изменение наклона рассчитанной кривой в момент времени, приблизительно равный 400 с, в противоположность гладкой опытной линии в той же области. Постепенное изменение наклона экспериментальной кривой объясняется влиянием сопротивления межфазной массопередаче. Однако в тех случаях, когда из теории равновесия следует, что составы среды и твердого вещества должны изменяться медленно, массообмен между фазами может проходить достаточно быстро, и теория локального равновесия окажется более точной. [21]
Случаи, в которых скорость определяется смещением температуры. Для кривой выделения, определяемой скоростью десорбции, наклон экспериментальной кривой, давление - время не должен зависеть от скорости нагревания. Наклон кривой выделения при любой заданной температуре должен быть линейной функцией наклона кривой температура - время. [22]
Уравнение ( VI-5), в отличие от уравнения ( VI-1), может быть использовано для непосредственной обработки экспериментальных данных х f ( n0), так как оно содержит те же переменные. Производная в уравнении ( VI-5) представляет собой тангенс угла наклона экспериментальной кривой к оси скоростей подачи и может быть найдена по экспериментальным данным методами графического или численного дифференцирования. [23]
Большая часть этих приближенных методов требует графического или численного дифференцирования исходной функции или связанных с ней функций. В некоторых методах в принципе могут быть использованы вторые и более высокие производные, но обычно ( за исключением отдельных случаев, когда кривизна резко изменяется) экспериментальные данные недостаточно точны, для того чтобы получить надежные значения производных выше второго порядка. Для определения наклона экспериментальных кривых, по мнению автора, предпочтительнее графические методы, хотя они и не вполне объективны. Процессы численного дифферен-цированпя подвержены флуктуациям, если исходные данные не сглажены до большего числа значащих цифр, чем это требуется для расчетов; однако они обладают тем преимуществом, что легко поддаются обычным методам обработки. [24]
Как уже отмечалось, для того чтобы применить уравнение Стирлинга, необходимо, чтобы как число шагов в направлении вправо п, так и число шагов влево ге, было достаточно большим по сравнению с единицей. Однако в области больших значений а цепные макромолекулы приобретают достаточно вытянутую конфор-мацию, так что либо п, либо ге уже нельзя считать достаточно большим по сравнению с единицей. Следовательно, как можно видеть из рис. 1.5, наклон экспериментальной кривой при приближении к ос 8 резко возрастает, в то время как теоретическая кривая даже при больших значениях а. В силу уравнения (1.38) аналогичная ситуация является характерной и для трехмерного случая. [25]
Подобное изменение кривых обусловлено не только полидисперсностью, но вследствие влияния последний, как это можно с уверенностью предполагать, кривые становятся более пологими. Ферри [63] недавно рассмотрел влияние характера МБР на релаксационные кривые с помощью некоторых экспериментальных методов. В итоге он пришел к выводу, что тангенс угла наклона экспериментальных кривых в общем изменяется менее резко и кривые смещены в область меньших частот па сравнению с теоретически рассчитанными кривыми. Можно ожидать, что подобное различие экспериментальных и теоретических кривых связано с полидисперсностью, поскольку компоненты системы с молекулярными весами, превышающими средний молекулярный вес образца, обусловливают появление гораздо более высоких значений времен релаксации. Отмеченное различие между кривыми будет тем сильнее выражено, чем шире распределение по молекулярным весам. [26]
Этот метод использовался для исследования адсорбции жидкостей и паров на кремнеземе. По мере того как бензол проникает в микропоры, его взаимодействие с поверхностью изменяет ход диэлектрической изотермы кремнезема. В более ранних исследованиях [102] было отмечено отсутствие закономерности в наклоне экспериментальной кривой, выражающей зависимость электрической емкости кремнезема от количества адсорбированной воды. [27]
Применяя описанный выше метод экстраполяции, мы пользовались стехиометрическими концентрациями. Но, как известно, серная кислота представляет собой умеренно сильный электролит и вторая стадия диссоциации протекает не до конца. Это обстоятельство подтверждается рис. 112, из которого видно, что наклоны экспериментальных кривых значительно больше, чем наклоны прямых, соответствующих предельному закону Дебая и Гюккеля для полностью диссоциированного электролита. [28]
На рис. 2 приведены две экспериментальные зависимости порогового отношения В / В0 от длительности импульса т для различных частот повторения: 1 - для 5 гц, 2 - 50 гц; 3 - теоретическая зависимость для 500 гц. Эксперимент подтвердил ожидающийся по формулам ( 2), ( 3) линейный в логарифмическом масштабе ход кривых. Несколько отличные от теоретических углы наклона экспериментальных кривых к оси абсцисс могут быть объяснены, по-видимому, адаптацией глаза к допороговому среднему значению U ( t) за счет обратной связи через односторонний преобразователь напряжения ( ОПН), не учитываемой в данном расчете для линейной модели. [29]
При более высоких температурах, особенно при 60, наклон кривых, полученных согласно Льюису и Рендаллу, больше теоретического наклона. Очевидно, что если учитывать требования теории, то истинные значения Е должны быть меньше соответствующих значений, получаемых первым методом. Такое согласование с теорией представлено на рис. 112 пунктирными линиями, направленными к величинам Е, полученным вторым методом. Где-то в области концентраций ниже 0 005 М экстраполяционные кривые должны иметь изгиб и наклоны экспериментальных кривых должны приближаться к наклонам, соответствующим предельному закону. Хотя наклоны представленных на рис. 112 экспериментальных кривых сильно отличаются от наклонов кривых, отвечающих предельному закону, мы полагаем, что это обусловлено тем простым фактом, что до сих пор не было получено надежных экспериментальных данных для изучаемых элементов при столь больших разбавлениях. Поскольку наличие у опытных кривых правильного теоретического наклона является необходимым, то несомненно, что величины Е, полученные вторым методом экстраполяции, более точны. [30]
Страницы: 1 2 3