Наклон - линия - регрессия
Cтраница 1
Наклон линии регрессии соответствует коэффициенту бета акции и выражает рискованность этой акции. [1]
Часто наклон линии регрессии можно предсказать из теоретического рассмотрения заданных величин. [2]
Да изменяет наклон линии регрессии и создает мультипликативную составляющую погрешности модели. [3]
Показателем, характеризующим доходность МТС, является угол наклона линии регрессии к оси абсцисс. Чем выше угол наклона, тем более доходна МТС. [4]
У по X и X по У, определяющие наклон линий регрессии в координатах X - У. [5]
В нашем примере 5 1 1 / зн1 27, значит, в показателях наклона линий регрессии различия несущественны. [6]
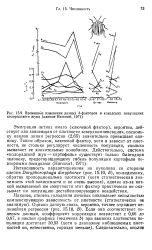 |
Временные изменения разных й-факторов в канадских популяциях колорадского жука ( данные Harcourt, 1971. [7] |
Эмиграция летних имаго ( ключевой фактор), вероятно, действует как зависящая от плотности сверхкомпенсация, поскольку наклон линии регрессии ( 2 65) значительно превышает единицу. Таким образом, ключевой фактор, хотя и зависит от плотности, не столько регулирует численность Популяции, сколько вызывает ее значительные колебания. [8]
Для этого случая представляет интерес определить координату ххг ( см. рис. 6 - 15), когда возрастающая мультипликативная погрешность аах достигает погрешности ал исходных экспериментальных данных и эффект уменьшения случайной погрешности от усреднения по п измерениям оказывается перекрытым возрастанием случайной погрешности от неопределенности угла наклона линии регрессии. [9]
Для этого случая представляет интерес определить координату х х ( см. рис. 6 - 15), когда возрастающая мультипликативная погрешность сах достигает погрешности од исходных экспериментальных данных и эффект уменьшения случайной погрешности от усреднения по п измерениям оказывается перекрытым возрастанием случайной погрешности от неопределенности угла наклона линии регрессии. [10]
Последний показатель, достойный упоминания, - это стандартная ошибка оценки коэффициента бета. Наклон линии регрессии, подобно любой статистической оценке, может отличаться от действительного значения, и стандартная ошибка показывает, насколько ошибочной может быть полученная оценка. [11]
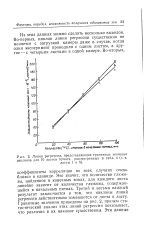 |
Линии регрессии, представляющие граничные значения. [12] |
Во-первых, наклон линии регрессии существенно не меняется с загрузкой камеры даже в случае, когда один эксперимент проводили с одним листом, а другие - с четырьмя листами в одной камере. [13]
Чем выше необъясненная дисперсия, тем больше разброс эмпирических точек, то есть выше риск системы. Отношение тангенса угла наклона линии регрессии к величине необъясненного с.к.о. является сводным показателем, характеризующим и доходность и риск системы. [14]
 |
Номограмма для. [15] |
Страницы: 1 2