Наклон - слой
Cтраница 1
 |
Пример слоистой структуры ( раствор поваренной соли. фотография из работы. [1] |
Наклон слоя к вертикали приводит к дополнительной стратификации. [2]
Наклон слоя создает в жидкости потенциально неустойчивую вертикальную стратификацию, что, в свою очередь, приводит в действие рэлеевский механизм неустойчивости. [3]
В этом и предыдущем параграфах рассмотрены два способа создания вертикальной стратификации, обусловленные наклоном слоя либо заданием продольного градиента. [4]
Отвечающий требованиям задачи код должен в наиболее сжатой форме определять: 1) углы наклона слоя к базовой ( координатной) оси; 2) число слоев, имеющих заданный угол наклона; 3) точный порядок расположения слоев. [5]
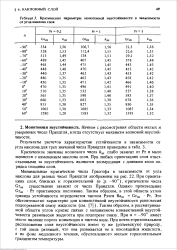 |
Критические параметры монотонной неустойчивости в зависимости от угла наклона слоя. [6] |
Критическое значение волнового числа km слабо зависит от Рг и мало меняется с изменением наклона слоя. При любых ориентациях слоя ответственными за неустойчивость являются возмущения с длинами волн порядка толщины слоя. [7]
В этом и следующем параграфах обсуждается влияние rta устойчивость конвективного течения вертикальной стратификации, создаваемой наклоном слоя. В наклонном слое, границы которого поддерживаются при разных температурах, градиент температуры имеет вертикальную составляющую. Если нагретая плоскость расположена сверху, то возникает потенциально устойчивая стратификация, оказывающая, в общем, стабилизирующее действие. Если же более высокую температуру имеет нижняя плоскость, то создается потенциально неустойчивая стратификация. Поэтому, кроме двух механизмов неустойчивости, рассмотренных в § 4, при достаточно большом градиенте температуры появляется еще один - конвективный ( рэлеевский) механизм, обусловленный подогревом снизу. При этом имеет место существенное взаимовлияние механизмов неустойчивости: наличие температурной стратификации меняет условия развития гидродинамических возмущений и тепловых волн; в то же время на фоне движущейся жидкости конвективная неустойчивость развивается не так, как в равновесии. [8]
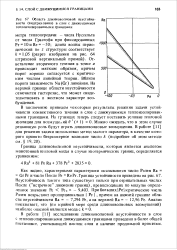 |
Область длинноволновой неустойчивости ( заштрихована в слое с движущимися теплоизолированными границами. [9] |
В работе [11] исследование длинноволновой неустойчивости в слое с теплоизолированными движущимися границами проведено в более общей постановке, учитывающей наклон слоя и наличие продольной прокачки. [10]
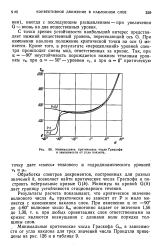 |
Минимальное критическое число Грасхофа в зависимости от угла наклона. [11] |
Результаты расчета показывают, что критическое значение волнового числа km практически не зависит от Р и мало меняется с изменением наклона слоя. [12]
В этом параграфе будет рассмотрена устойчивость стационарного конвективного течения в вертикальном слое при наличии, кроме поперечной разности температур, еще и продольного температурного градиента. Так же, как и наклон слоя к вертикали, продольный градиент создает стратификацию, устойчивую или неустойчивую в зависимости от его направления. Следует, однако, отметить существенное отличие в двух способах создания стратификации. В случае наклонного слоя стратификация не влияет на профиль скорости. Наличие же продольного градиента не только создает стратификацию, но и существенно изменяет форму и интенсивность основного течения, что, в свою очередь, сильно влияет на устойчивость. [13]
 |
Подрезка поверхности нижней полуформы. [14] |
При этом конец гладилки врезают на глубину 10 - 30 мм ( в зависимости от величины формы) на расстоянии 40 - 100 мм от края рабочей полости и, соблюдая указанные размеры, подрезают полуформу по всему периметру. Гладилку при подрезе держат так, чтобы наклон подрезаемого слоя всегда был обращен к рабочей полости формы. Для форм в опоках размерами до 500X500 лш глубина подрезки должна быть равной 10 - 15 мм, для более крупных форм - до 30 мм. При сборке подсушиваемых, сухих и химически твердеющих форм плотность, стыка полуформ достигается проложением слоя прокладочной глины или асбестового шнура диаметром 5 - 10 мм. [15]
Страницы: 1 2