Ханойская башня

Cтраница 1

Ханойская башня для случая четырех дисков. [1]

Ханойская башня) Каждый подающий надежды ученый должен познакомиться с некоторыми классическими задачами, а Ханойская башня ( см. рис. 5.18) - это одна из наиболее известных классических задач. Легенда гласит, что в храме на Дальнем Востоке священники пытаются переместить башню из дисков с одной стойки на другую. [2]

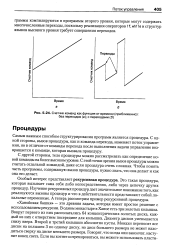Счетчик команд как функция от времени ( приближенно. без переходов ( а. с переходами ( б. [3]

Ханойская башня - это древняя задача, которая имеет простое решение с использованием рекурсии. [4]

Ханойская башня - это не единственная рекурсивная процедура, любимая многими компьютерщиками. [5]

Задача о Ханойской башне является типичным примером ситуации, когда легко отыскивается рекурсивный метод решения, но весьма трудно ( по крайней мере, доказать правильность метода) находить итеративное решение. [6]

Пример с Ханойскими башнями типичен. Изучение ( конечной) таблицы с экспериментальными данными задачи часто подсказывает нам гипотетическое утверждение 5 ( п), и мы ожидаем, что оно справедливо для всех натуральных чисел. Математическая индукция предлагает систематический подход к доказательству многих таких утверждений. [7]

Основные алгоритмы типа. [8]

Задача о ханойских башнях, рисование линейки и фракталы весьма занимательны, а связь с двоичным числами поражает, однако все эти вопросы интересуют нас прежде всего потому, что облегчают понимание одного из основных методов разработки алгоритмов - деление задачи пополам и независимое решение одной или обеих половин задачи; возможно, это - наиболее важная из подобного рода технологий, рассматриваемых в книге. [9]

С задачей о Ханойской башне связана легенда, определившая ее название. Согласно этой легенде в одной восточной стране мудрецы, работая день и ночь, должны перенести 64 диска с одного стержня на другой, выполняя при этом вышепоставленные ограничения на взаиморасположение дисков. [10]

Предложите итеративную стратегию для ханойской башни, которая позволит эффективно решать задачу без предварительной генерации программы. [11]

Применительно к задаче о ханойских башнях использование соответствия с - разрядными числами - простой алгоритм решения задачи. [12]

Зала ч а о ханойских башнях, рисование линсйкн и фракталы ьесьм занимательны h и связь с лнончным чнс-лами поражает h вднако все эти пол росы интересуют прежде Ficcto потому, что облегчают понимание OJIHUJO основных методов разработки биоритмов - деление задачи пополам и независимое решение одной или обеих половин задачи: возможно, это - наиболее нажили из [ вдюб-ного рода технологии рассматриваемых п книге. [13]

Ниже приводится программа задачи о Ханойской башне я результат для перемещения 5 дисков. [14]

Многие широко известные задачи ( типа Ханойская башня, Миссионеры и людоеды и др.) могут быть представлены в виде задач с ограничениями. [15]

Страницы: 1 2 3 4