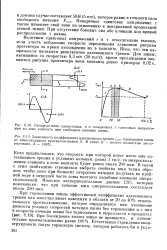
Поперечное сдвиговое напряжение
Cтраница 1
Поперечное сдвиговое напряжение т также изменяет свой знак по отношению к центральной продольной осевой линии. При отсутствии боковых сил обе площади под кривой распределения т равны. [2]
Принимается, что поперечные сдвиговые напряжения воспринимаются только слоями изотропного связующего, а слои с армирующими волокнами являются абсолютно жесткими на сдвиг. [3]
Как показывают результаты экспериментов [3, 54, 66 68, 71, 144, 162, 196, 208, 242, 248, 250, 257], именно разрушение от поперечных сдвиговых напряжений во многих случаях лимитирует несущую способность конструкций из композитных материалов. [4]
В работах [80, 106, 150, 217, 254, 259] использовались гипотезы С. П. Тимошенко, которые, хотя и учитывают поперечные сдвиговые напряжения, но граничным условиям не удовлетворяют. Поэтому применение уравнений изгиба, основанных на указанных гипотезах, может привести к значительным погрешностям при определении поперечных сдвиговых напряжений, которые являются наиболее опасными для конструкций, армированных высокопрочными волокнами. [5]
Наибольшее отклонение неклассического решения от решения, найденного с привлечением модели жестких нормалей, достигается при законе распределения поперечных сдвиговых напряжений по толщине, близком к параболическому. [6]
Из табл. 6.3.3, 6.3.4 видно также, что наибольшее отклонение рассматриваемых расчетных величин от решения, найденного с привлечением модели недеформируемых нормалей, вновь достигается при законе распределения поперечных сдвиговых напряжений по толщине, близком к параболическому. [7]
Подчеркнем, что и в этом примере снижение расчетных значений разрушающих нагрузок никак не связано с пренебрежением ( при расчете по классической теории) в квадратичной форме Мизеса (2.2.3) поперечными сдвиговыми напряжениями. Как выявлено расчетами [12], разрушение связующего и армирующих волокон инициируется в защемленном сечении х 0 оболочки, соответственно на поверхности z h внешнего слоя и на поверхности z О внутреннего слоя, где поперечные сдвиговые напряжения равны нулю в силу условий нагружсния, причем в этих точках основной вклад в квадратичную форму (2.2.3) вносят осевые напряжения. Следовательно, и в этом примере снижение расчетных значений разрушающих нагрузок обусловлено существенно иным, по сравнению с классическим, распределением нормальных напряжений, особенно в зонах краевых закреплений. [8]
Через Лгу Р ( г) а р & р а обозначим аналогичные величины, найденные без учета поперечных сдвиговых деформаций. Следует отметить, что в рамках классической теории оболочек поперечные сдвиговые напряжения, фигурирующие в квадратичной форме Мизеса (2.2.3), строго говоря, неопределены. [9]
Как видно из (3.1.7), (3.1.8), поперечные касательные напряжения т3, будучи непрерывными функциями координаты z всюду в теле оболочки, в том числе и на поверхностях раздела z А. А; тем самым удовлетворены условия (3.1.3) - (3.1.5) для поперечных сдвиговых напряжений. [10]
В первой главе на основе принципа возможных перемещений получены уравнения равновесия для произвольных оболочек и естественные краевые условия. Их вывод базируется на кинематических и физических гипотезах, которые позволяют учитывать поперечные сдвиговые напряжения, удовлетворяющие необходимым граничным условиям па лицевых поверхностях оболочки. Физические соотношения для армированного материала и критерий прочности для него построены на основе структурного подхода. Дана математическая формулировка структурного Крите - - рия прочности армированных оболочек и предложен конструк - - тивный метод определения гиперповерхности разрушения оболочки в пространстве параметров внешнего воздействия. [11]
В работах [80, 106, 150, 217, 254, 259] использовались гипотезы С. П. Тимошенко, которые, хотя и учитывают поперечные сдвиговые напряжения, но граничным условиям не удовлетворяют. Поэтому применение уравнений изгиба, основанных на указанных гипотезах, может привести к значительным погрешностям при определении поперечных сдвиговых напряжений, которые являются наиболее опасными для конструкций, армированных высокопрочными волокнами. [12]
От последнего недостатка свободны уравнения теории многослойных оболочек регулярного строения, собранных из чередующихся между собой тонких жестких несущих слоев и мягких слоев-заполнителей. Система допущений, используемых в этой теории, такова: для несущих жестких слоев принимается модель недеформируемой нормали ( в рамках этой модели поперечные сдвиговые напряжения, строго говоря, неопределены), для слоев-заполнителей - модель прямой линии. Сформулируем соответствующую этим допущениям систему уравнений и притом сразу для общего случая произвольного расположения г жестких несущих слоев и m - г слоев-заполнителей в многослойном пакете. [13]
Отсюда, как и в случае изотропных слоистых оболочек, заключаем, что из всех рассматриваемых характеристик напряженно-деформированного состояния наиболее чувствительной к виду функции / ( z) является осевое напряжение а, тогда как влияние вида этой функции на все остальные расчетные величины невелико. Из табл. 6.3.5, 6.3.6 видно также, что наибольшее отклонение рассматриваемых расчетных величин от решения, найденного с привлечением модели недеформируемых нормалей, вновь достигается при законе распределения поперечных сдвиговых напряжений по толщине, близком к параболическому. [14]
Наконец, через Л-iV т бозначим давления начального разрушения несущих слоев, вычисленные по классической теории. При рассматриваемых условиях все характеристики напряженно-деформированного состояния пластинки являются нечетными функциями нормальной координаты z и потому Р 1 Р ( 1, Р, п Р ( 1у Следует отметить также, что поперечные сдвиговые напряжения, фигурирующие в квадратичной форме Мизеса (2.2.3), в рамках классической теории, строго говоря, неопределены. [15]
Страницы: 1 2