Релаксационное автоколебание

Cтраница 1

Релаксационные автоколебания - автоколебания нелинейных систем, закон таких автоколебаний резко отличен от гармонического. Примеры релаксационных автоколебаний: сифон, колебания в схеме с неоновой лампой. [1]

Динамическая модель Ван-дер - Поля для демонстрации фрикционных автоколебаний. [2]

Релаксационные автоколебания, возникающие в системах с трением, обычно далеки по форме от гармонических колебаний; квазигармонические фрикционные автоколебания по частоте равны собственным частотам, а их форма близка к форме собственных колебаний динамической системы, участвующей в колебаниях. [3]

Релаксационные автоколебания, которые наблюдаются при бурении любыми типами долот, возникают при периодическом высвобождении ( по мере заглубления долота в породу) энергии, аккумулируемой трением замков о скважину, при разгрузке части веса колонны на стенки ствола. Наиболее значительными среди них являются автоколебания, которые возникают в сжатой части колонны, пространственно деформированной в виде винтовой спирали. Частота их варьируется от субинфразвукового до инфразву-кового диапазона. [4]

Свойство релаксационных автоколебаний легко и устойчиво синхронизоваться использовалось Ван-дер - Полем и Ван-дер - Марком [1927] для деления частоты. [5]

О релаксационных автоколебаниях при нестационарной двухфазной фильтрации / / Нефтепромысловое дело. [6]

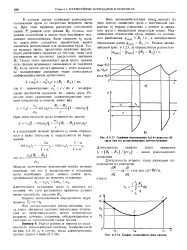S. 23. Графики перемещения ( а и скорости ( п грузя при его релаксационных автоколебаниях.| S. 24. График нелинейной силы трения. [7]

При релаксационных автоколебаниях, когда закон движения системы значительно отличается от синусоидального, могут наблюдаться разрывы, которые, например, обнаруживаются в системах со значительной силой трения. [8]

Популярной моделью релаксационных автоколебаний служит система типа накопление - сброс. [9]

Рост амплитуды релаксационных автоколебаний с увеличением скорости, характерный для колебаний гармонического типа, не может быть объяснен статической зависимостью силы трения от времени неподвижного контакта. В зоне скоростей, при которых оно мало по сравнению с периодом автоколебаний системы, движение системы должно определяться закономерностями, свойственными колебаниям гармонического типа. [10]

Если в области релаксационных автоколебаний частота их непрерывно, возрастает по мере увеличения скорости, то и в области колебаний гармонических она также не остается постоянной. Однако здесь в подавляющем большинстве случаев наблюдается иная тенденция. Начиная от скорости, при которой происходит переход от одного вида колебаний в другой, до первого максимума частота автоколебаний, как правило, снижается. Это явление хорошо видно на графиках фиг. В дальнейшем, если колебания не затухают и появляется новый максимум, частота автоколебаний в большинстве случаев возрастает, но никогда не превышает меньшей из парциальных частот системы. [11]

Временная эволюция механического осциллятора типа накопление - сброс, показанного на Вода накапливается до тех пор, пока не достигнет порогового уровня, показанного пунктирной линией ( а, после чего уровень воды быстро спадает до нуля. Это соответствует импульсу на графике зависимости потока воды через сифон от времени ( Ь. [12]

Мы начнем наше рассмотрение релаксационных автоколебаний с простейшей механической модели [ Пановко и Губанова 1964 ], схема которой показана на рис. 2.12. Основной элемент этой системы - сосуд, медленно заполняемый водой. Когда уровень воды достигает порогового значения, сосуд быстро опорожняется, и начинается новый цикл колебаний; энергия насоса, обеспечивающего постоянную подачу воды, преобразуется в колебания уровня воды в сосуде. Так как в течение каждого периода колебаний вода медленно накапливается, а затем почти мгновенно удаляется из сосуда, такие системы часто называют осцилляторами типа накопление - сброс. Если мы построим график зависимости уровня воды в сосуде и потока через сифон от времени ( рис. 2.13), то интервалы медленных и быстрых движений будут хорошо видны. [13]

Далее мы рассмотрим особенности синхронизации релаксационных автоколебаний и рассмотрим, что происходит с захватом частоты в присутствии шума. По ходу изложения будут приведены различные экспериментальные примеры. Наконец, мы обсудим некоторые явления, имеющие отношение к синхронизации, такие как хаотизация и подавление автоколебаний сильным внешним воздействием, а также эффект действия периодической силы на возбудимые системы и явление стохастического резонанса. [14]

В колоннах с затопленной насадкой могут возникнуть релаксационные автоколебания. Это наблюдается, когда всплывание газовых пузырей под действием разности плотностей не может обеспечить прохождения заданного количества газа. Газ задерживается в нижней части колонны, и наряду с мелкими газовыми пузырями формируются крупные газовые агрегаты, которые не дробятся на насадке и поднимаются в колонне со скоростью, превышающей скорость свободного всплывания отдельных мелких пузырей газа. Образование газовых агрегатов и выход их из слоя пены вызывают пульсации и выброс жидкости выше слоя насадки. [15]

Страницы: 1 2 3