Неравномерность - движение - цепь
Cтраница 1
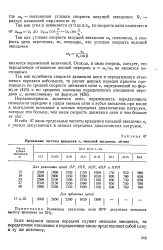 |
Предельные частоты вращения i меньшей звездочки, об / мин. [1] |
Неравномерность движения цепи, переменность передаточного отношения передачи и удары звеньев цепи о зубья звездочек при входе в зацепление вызывают в цепных передачах динамические нагрузки, которые тем больше, чем выше скорость движения цепи и чем больше ее шаг. [2]
Неравномерность движения цепи обусловливает возникновение динамических нагрузок на цепь, которые должны учитываться при детальных расчетах конвейеров. [3]
Неравномерность движения цепи, переменность передаточного числа передачи и удары звеньев цепи о зубья звездочек при входе в зацепление вызывают в цепных передачах динамические нагрузки, которые тем больше, чем выше скорость движения цепи и чем больше ее шаг. [4]
 |
Профиль зубьев звездочек в сечении ( плане. [5] |
Динамические нагрузки вызываются неравномерностью движения цепи и ведомой звездочки, технологическими погрешностями, допущенными при изготовлении и монтаже цепи и звездочек. На динамику цепных передач неблагоприятно влияет относительное удлинение цепи в результате износа ее шарнирных соединений. [6]
Динамические нагрузки вызываются неравномерностью движения цепи и ведомой звездочки, технологическими погрешностями, допущенными при изготовлении и монтаже цепи и звездочек. На динамику цепных передач неблагоприятно влияет относительное удлинение цепи в результате изнашивания ее шарнирных соединений. Длина ведущей ветви цепной передачи изменяется также вследствие радиальных биений валов и зубчатых венцов, а также наличия зазоров между ступицей звездочки и валом. В связи с этим погрешности изготовления и монтажа цепных передач должны быть в пределах допускаемых значений. На практике при расчете цепных передач буровых установок динамические нагрузки учитываются коэффициентом перегрузки. [7]
Таким образом, для достижения минимальной неравномерности движения цепи и звездочек, снижения динамических нагрузок, повышения долговечности и надежности цепных передач необходимо обеспечить синфазное движение звездочек. Для этого необходим правильный геометрический расчет цепного контура. [8]
Шарнирный четырехзвенник привода механизма погрузки, увеличивая степень неравномерности движения цепи, в то же время не позволяет рационально использовать время выстоя каретки для осуществления захвата брикета и подъема его на нужную высоту. Таким образом, полезную работу узел нагрузки совершает только за часть оборота кривошипа 28 ( около половины оборота), другая же часть оборота используется для холостого возвращения собачки 32 в исходное положение. [9]
В ведущей ветви цепи скоростных передач возникают дополнительно циклически действующие динамические силы, вызванные неравномерностью движения цепи и ведомой системы. Эти силы в полной мере зависят от жесткости цепи и от маховых масс, приведенных к ведомому валу, и их следует учитывать при проектировании ответственных цепных передач, поскольку динамические силы влияют на усталостную прочность звеньев цепи. [10]
Недостатками передач с гибкой связью является непостоянство и колебание передаточного отношения из-за проскальзывания ремня и неравномерность движения цепи и зубчатого ремня, малая долговечность гибкого звена. [11]
 |
Схема для расчета натяжений цепи конвейера. [12] |
Динамические нагрузки на тяговую цепь и другие элементы оборудования возникают при пуске конвейера вследствие преодоления сил инерции движущихся масс и изменения коэффициентов сопротивления движению при переходе от покоя к движению; при неравномерности движения цепи ведомой приводной звездочкой; при возникновении ускорений цепи на горизонтальных и вертикальных поворотах, а также при захвате толкателем неподвижной тележ ки с грузом. Особую группу составляют аварийные динамические нагрузки, действующие при случайном застопорении конвейера и обрыве цепи. [13]
 |
Схема движения цепи по приводной звездочке. [14] |
При постоянной угловой скорости приводной звездочки ( или блока с прямолинейными гранями) скорость движения цепи не остается постоянной, а периодически изменяется ( пульсирует) по определенному кинематическому закону. Длительность периодов неравномерности движения цепей равна временя поворота приводной звездочки на центральный угол, соответствующий одному звену цепи. [15]
Страницы: 1 2