Неразрешимость - проблема
Cтраница 1
Неразрешимость проблемы гомеоморфии / / Докл. [1]
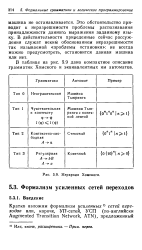
Неразрешимость проблемы остановки - прямое следствие того, что вычисляемая универсальной машиной U функция обязательно частичная. Точнее, в § 2.2.10 показано существование программы Р с кодом Р п, таким, что U ( п, п) не определено. [2]
Неразрешимость проблем эквивалентности и пустоты языков следует из теоремы 5.3 и неразрешимости этих проблем для рекусивно перечислимых языков. [3]
Неразрешимость проблемы сводимости теории алгоритмов, Докл. [4]
Неразрешимость проблемы распознавания применимости нормального алгоритма к слову в А означает отсутствие общего метода, который для любого алгоритма и любого слова в А мог бы дать интересующий нас ответ. Ограничивая класс алгоритмов или класс обследуемых слов, или и то и другое, можно в некоторых случаях получить разрешимые массовые проблемы. [5]
Черч доказал неразрешимость проблемы разрешения [ Черч, 1936 ] и что в настоящее время доказана неразрешимость ряда куда более скромных массовых математических проблем. Но ведь все эти результаты основаны на том или ином уточнении понятия алгорифма ( единого общего метода), например на понятии рекурсивной функции, и на предположении об адекватности этого уточнения, например на тезисе Черча, утверждающем, что рекурсивность равносильна вычислимости. Ясно, что без копания в понятии алгорифма никакое доказательство невозможности разрешающего алгорифма не пройдет. Если вы не хотите признать тезис Черча или что-нибудь в этом роде, то вы вынуждены будете согласиться с тем, что все ваши расхождения с господином Классом зависят от состояния наших знаний в настоящий момент. Все ваши антиклассическне высказывания придется тогда рассматривать как истины de facto, а не de jure. [6]
Аналогично доказывается неразрешимость проблемы ограниченности в классе сетей с приоритетами и проблемы достижимости в обоих классах обобщенных сетей. [7]
Простое доказательство неразрешимости проблемы истинности можно дать с использованием МНР, хотя это требует некоторого знакомства с исчислением предикатов. Читателю, который не знаком с началами логики предикатов, мы советуем пропустить приведенный ниже набросок доказательства. [8]
В работе [7] доказана неразрешимость проблемы эквивалентности в классе схем программ, близком к классу конечных однозначных последовательных схем. [9]
Заметим еще, что неразрешимость проблемы применимости нормальных алгоритмов легко переносится на любой другой достаточно четко описанный класс алгоритмов, если только для алгоритмов этого класса можно придумать такой способ кодирования, при котором коды алгоритмов оказывались бы допустимыми исходными данными для таких алгоритмов. [10]
 |
Иерархия Хомского. [11] |
Это обстоятельство приводит к неразрешимости проблемы распознавания принадлежности данного выражения заданному языку. В действительности приведенные сейчас рассуждения служат неким обоснованием неразрешимости так называемой проблемы остановки: не всегда можно предусмотреть, остановится данная машина или нет. [12]
Пост [1947] и Марков [1947] доказали неразрешимость проблемы разрешимости, представляющей интерес в качестве первого примера, в котором рассматривается проблема, возникшая не в области логики или оснований математики. [13]
Чтобы убедиться в этом, достаточно показать неразрешимость более узкой проблемы, а именно - не существует алгоритма, который для любого счетчика может установить, будет ли его начальное нулевое значение изменено хотя бы один раз, т.е. является ли счетчик 0-ограниченным или нет. [14]
Перед тем, как перейти к приложениям неразрешимости проблемы равенства слов в некоторых представлениях, мы опишем другой подход к построению групп с неразрешимой проблемой слов, принадлежащий Хигману [98]; этот подход вскрывает глубокую связь между идеями вычислимости и конечной представимостью групп. Множество А слов над SB называется эффективно перечислимым, если существует некоторая эффективная процедура, перечисляющая элементы А. Следует подчеркнуть, что это вовсе не означает, что элементы множества А перечисляются таким образом, что для произвольного слова возможно за конечное число шагов установить, лежит оно в А или нет. Мы оставим интуитивным понятие эффективной процедуры и заметим только, что его точное определение аппелирует к понятиям наподобие машины Тьюринга. [15]
Страницы: 1 2 3 4