Несовершенство - модель
Cтраница 1
Несовершенство модели с типовым блоком обусловлено прежде всего гипотезой о равенстве давления по всей поверхности отдельно взятого пористого блока, что заведомо неприемлемо при совпадении или близости значений фильтрационных параметров составляющих сред. Диапазон применимости обеих моделей, по существу, ограничен неравенствами (5.4), к тому же сугубо приближенно. [1]
 |
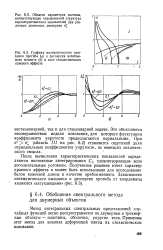
Качественный вид изменения скорости прилипания в различных моделях. [2] |
Несовершенство моделей фильтрования проявляется также в том, что гидравлические расчеты на базе уравнения (4.6) ведутся независимо от динамики осветления. Остановимся кратко на гидравлике фильтрования, поскольку детальное рассмотрение этого вопроса выходит за рамки книги. [3]
Понимая несовершенство исходной гидрохимической модели, представляемой системой уравнений (2.18) - (2.22), можно тем не менее увидеть ее существенное достоинство в том, что уже в настоящее время она реально может быть обеспечена необходимой параметрической базой. [4]
Это объясняется несовершенством модели основания, для которого флуктуации коэффициента упругости предполагаются нормальными. При tf2 l ( область / / / на рис. 6.2) становится ощутимой доля отрицательных коэффициентов упругости, не имеющих механического смысла. [6]
Четвертая глава посвящается обсуждению несовершенств моделей классических теорий поверхности, приводятся данные литературных источников, рассматривающих поверхность как фрактальный объект и явления на границе раздела фаз в рамках концепции неравновесных самоорганизующихся процессов. В заключение предлагается гипотеза о существовании дробно-размерного поверхностного слоя, обеспечивающего переход между объемами фаз с целой пространственной размерностью. [7]
Указанные недостатки свидетельствуют о несовершенстве модели, но не опровергают ее главного вывода о нестационарности Вселенной. [8]
 |
Распределения концентрации вытесняющего нефтепродукта в смеси для различных моментов времени. [9] |
Конечно, эффект этот является результатом несовершенства модели, однако стремление концентрации к 1 слева и - к 0 справа происходит так быстро, что зона, в которой происходит переход от одного нефтепродукта к другому, имеет практически ограниченные размеры. [10]
Обычно несоответствие эмпирических данных той или иной модели воспринимается как несовершенство модели и рассматривается как повод для ее уточнения путем введения какого-нибудь дополнительного параметра. Уникальность моделей семейства Раша состоит в том, что они задают определенный механизм преобразования формальных наблюдений за исходом событий в объективные измерения на метрической шкале латентных стимулов этих событий. Но метрические свойства продукции возможны лишь при условии, что исходные материалы удовлетворяют определенным требованиям. [11]
Заметим, что систематические погрешности могут быть связаны с каждым из элементов процесса измерений: несовершенством модели объекта измерения, несовершенством метода, средством измерения, изменением внешних условий, личными качествами наблюдателя. [12]
В (8.3) и (8.4) все параметры объектов принимаются равнозначными и равнонадежными, что существенно упрощает задачу за счет несовершенства отображающей модели. Тем не менее для ориентировочной, предварительной оценки такой подход допустим. [13]
Обычно если речь идет о несуперко-ротких импульсах, длина которых много больше размеров пузырей и расстояний между ними, это несовершенство модели, связанное в основном с использованием уравнения Рэлея - Ламба, не играет существенной роли, ибо доля энергии таких импульсов, приходящаяся на высокочастотную часть ( ш сос) спектра, мала, и поэтому амплитуда предвестника также пренебрежимо мала. На самом деле эта амплитуда еще и быстро затухает на расстояниях порядка расстояний между пузырьками 2R из-за акустической разгрузки высокочастотных волн сжатия па пузырьках, причем в процессе такой разгрузки размер пузырьков измениться практически но успевает. [14]
Как видно из приведенного обзора, несмотря на то, что экспериментально вязкостные измерения наиболее просты по сравнению, например, со светорассеянием, интерпретация данных достаточна сложна, во-первых, из-за несовершенства модели для описания поведения макромолекуля: р ого клубка в растворе, во-вторых, - их сложной взаимосвязи с термодинамическими параметрами системы полимер - растворитель, которые тоже еще находятся в стадии теоретической разработки и экспериментальной проверки. [15]
Страницы: 1 2 3