Рассматриваемая неустойчивость

Cтраница 1

Рассматриваемая неустойчивость, приводящая к резкому возрастанию тепловыделения внутри системы за счет протекающих в ней процессов тепловыделения, носит название теплового взрыва. [1]

Рассматриваемая неустойчивость характерна для достаточно длинноволновых возмущений. Коротковолновые возмущения стабилизируются избыточным давлением частиц на вогнутую поверхность шланга. [2]

Таким образом рассматриваемая неустойчивость проявляется в том, что эти возбуждения нарастают во времени, превращаясь в конечном счете в застывшие волны в распределении плотности. [3]

Очевидно, что развитие рассматриваемых неустойчивостей наиболее вероятно в области, где G максимально. В то же время из табл. 4.1 видно, что в обеих рассмотренных моделях экзосферы G меняется с высотой в достаточно большом Диапазоне. [4]

Распределение потенциала поперек наклонного двойного слоя в горячей плазме. [5]

Из выражения (3.27) видно, что если плотность холодных ионов мала ( так, что щ HO), порог развития рассматриваемой неустойчивости резко возрастает. Таким образом, наличие относительно холодных ионов является необходимым условием развития ионно-циклотронной неустойчивости и соответственно появления наклонных двойных слоев. [6]

В работе [6] методом размерностного анализа был введен критерий наступления рассматриваемой неустойчивости Re, 9у ( 0 - время релаксации, у - скорость сдвига), названный эластическим критерием Рейнольдса, который представляет собой меру отношения упругих и вязких сил в потоке упруго-вязкой жидкости. [7]

Изменение формы поры в процессе диффузионного роста. дендритный рост. [8]

Оказалось, что при достаточно больших скоростях диффузионного роста возмущения по контуру поры могут стать неустойчивыми, что приводит, к возникновению пальцеобразных полостей, которые развиваются в плоскости границы впереди отставшего основного контура поры. Поскольку поверхностная диффузия стремится сглаживать возмущения по контуру поры, условия существования рассматриваемой неустойчивости сильно зависят от соотношения между скоростями диффузии на поверхности и по границам. [9]

С этим обстоятельством связана относительно простая форма вторичных течений, которые удается описать с помощью единственной медленно меняющейся в пространстве и во времени комплексной функции, называемой амплитудной функцией. В низшем пордяке по малому параметру надкритичности ( Gr - - Grm) 2 амплитудная функция, независимо от физической природы рассматриваемой неустойчивости, подчиняется некоторому универсальному уравнению, причем от параметров конкретной задачи зависят лишь численные значения небольшого числа коэффициентов. [10]

Формирование ударной волны в ударной трубе. [11]

Однако если g ( М0) 0, то возмущение формы плоского фронта растет - отставшие участки будут все более отставать, выдавшиеся вперед - убегать все дальше. При этом гофрировка фронта делается все более явно выраженной и переходит в течение более сложного вида. По своему проявлению рассматриваемая неустойчивость сходна с рэлей-тейлоровской: здесь ударно-сжатое вещество играет роль тяжелой жидкости, сжимаемой легкой жидкостью - невозмущенным потоком. [12]

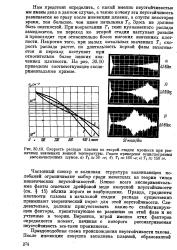Скорость распада плазмы во второй стадии процесса при различных значениях ионноя температуры. Рядом приведены осциллограммы высокочастотных шумов, а Т - х, 50 зе. б Т zz 100. в ] TI ж 150 зв. [13]

Частотный спектр и волновая структура возникающих колебаний ограничивают выбор среди известных из теории типов кинетических неустойчивостей. Ближе всего экспериментальные факты отвечают дрейфовой моде конусной неустойчивости ( см. § 15) вблизи порога ее возбуждения. Правда, градиенты плотности плазмы в начальной стадии распада существенно превышают теоретический порог для этой неустойчивости. Следовательно, должны присутствовать какие-то стабилизирующие факторы, препятствующее ее развитию на этой фазе и не учтенные в теории. Вероятно, игрой именно этих факторов определяется момент, начиная с которого рассматриваемая неустойчивость все-таки проявляется. [14]

Страницы: 1