Дипольная неустойчивость

Cтраница 1

Дипольная неустойчивость оказывается весьма интересной прежде всего в следующих двух основных аспектах. Во-первых, системы, которые считают традиционно симметричными и не обладающими дипольным моментом, могут проявить свойства, присущие системам с дипольным моментом. [1]

При слабой дипольной неустойчивости, когда б kT, как указывалось, электрические свойства системы приближаются к ожидаемым для симметричных молекул, не имеющих собственного дипольного момента. Если при этом 8 не очень велико, то с повышением температуры начнет проявляться температурная зависимость поляризуемости, интерпретируемая как появление ( и возрастание) собственного дипольного момента. Обнаружение этого эффекта представляется одной из интересных экспериментальных задач. [2]

Отсюда следует принципиальный вывод, что с учетом дипольной неустойчивости деление молекул на твердодипольные и симметричные по их поведению в электрическом поле ( по температурной зависимости поляризации) условно: оба типа поведения - линейная зависимость поляризуемости от 1 / Т и ее независимость от Т - присущи одним и тем же молекулам в различных областях температур ( рис. VIII. Последние же определяются величиной дипольной неустойчивости ( ср. [3]

Существует два значения этого параметра, которые разграничивают дипольную неустойчивость, неустойчивость с заряженным слоем и абсолютную устойчивость полупроводника с ОДП. [4]

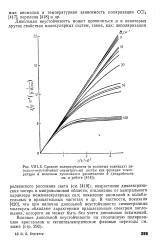Средние поляризуемости ( в условных единицах да-польно-неустойчивых симметричных систем как функция температуры и величины туннельного расщепления б ( подробности в работе. [5]

В частности, показано [420], что при наличии дипольной неустойчивости симметричные молекулы обладают характерным вращательным спектром поглощения, которого не может быть без учета дипольных искажений. [6]

Ниже рассматривается другой иллюстрирующий это правило пример, связанный с дипольной неустойчивостью молекул. [7]

В предельном случае ( 6 / &71) - 0 ( сильная дипольная неустойчивость, слабое туннелирование, высокие температуры) р р и верны обычные соотношения. В промежутке между этими предельными значениями р монотонно убывает от значения р до нуля. [8]

Первое значение параметра n0L, составляющее примерно 2 5 1011 см 2 [4], является граничным при переходе из области дипольной неустойчивости в область неустойчивости с заряженным слоем. Физически значение критерия существования дипольного слоя n0L s 2 5 1011 см-2 можно рассмотреть на следующем примере. Пусть распределение концентрации электронов и напряженности электрического поля вдоль домена имеет вид, изображенный па рис. 8.6. Протяженность ( длина) отрицательного объемного заряда такого домена обычно значительно меньше положительного. Это связано с тем, что ограничивает концентрацию избыточных электронов лишь диффузия электронов из области отрицательного объемного заряда. Для того чтобы компенсировать отрицательный объемный заряд, положительно заряженная часть диполя должна быть достаточно протяженной, поскольку концентрация положительных ионов примеси постоянна. Следовательно, домен не может быть бесконечно тонким, и для данной концентрации п0 он обладает минимальной длиной, при которой еще возможно его существование и движение через кристалл. [9]

Два минимума адиабатического потенциала для молекулы аммиака и инверсионное расщепление. [11]

Это возможно при наличии центра инверсии в случае псевдовырождения между двумя электронными состояниями противоположной четности или в случае Т - - задачи для систем без центра инверсии. Напомним, что в системах с центром инверсии обычный эффект Яна - Теллера на вырожденных термах не может привести к дипольной неустойчивости. [12]

Страницы: 1