Номер - итерация
Cтраница 3
Во избежание громоздкости индекс k - номер итерации - здесь опущен. [31]
В и т не зависят от номера итерации k, то процесс называют стационарным. [32]
В цикле по t ( t - номер итерации) осуществляется процедура, описанная в пп. [33]
В табл. 1 показаны в зависимости от номера итерации v величины min ( x, g) и XE. [34]
Верхний индекс у Ly ( 2) обозначает номер итерации. [35]
Верхние индексы в ( 11 12) обозначают номер итерации. [36]
 |
Результат применения асинхронного алгоритма прореживания. символ - - удаленные пикселы, символ О - пикселы остова. [37] |
В данном алгоритме это легко предусмотреть, использовав номер итерации в качестве значения метки каждого пиксела при его первом заключении в категорию основных. Для этого потребуются дополнительные затраты памяти, однако во всех остальных отношениях реализация этой модификации алгоритма оказывается очень простой. Символ С обозначает число итераций, увеличенное на пять, и поэтому в качестве меток для пикселов, принадлежащих остову, могут использоваться числа не пересекающиеся со значениями меток, необходимых для выполнения основных операций алгоритма. На рис. 9.6 приведен пример применения описанного алгоритма к дискретизированным изображениям буквенно-цифровых символов. [38]
В формулах (8.12) - (8.15) верхний индекс соответствует номеру итерации. [39]
Чтобы они были устойчивыми к малым изменениям исходных данных, номер итерации г, которая принимается за приближенное решение, надо брать согласованным с уровнем погрешности исходных данных. [40]
Здесь, как и в дальнейшем, верхний индекс означает номер итерации, а через xQ обозначено исходное ( начальное) приближение, с которого начинается итерационный процесс. [41]
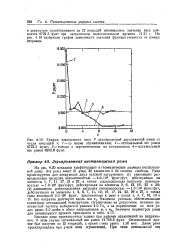
На рис. 4.19 изображен график зависимости значений функции стоимости от номера итерации. [43]
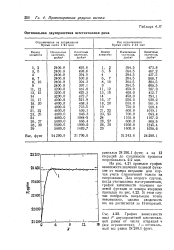 |
График зависимости веса Р двухпролетной шестиэтаж - - ной рамы от числа итераций v 16 ( все ограничения. / - оптимальный вес равен 24290. 1 фунт.. [44] |
На рис. 4.21 приведен график зависимости значений целевой функции от номера итерации для случая учета ограничений только на напряжения. Для второго случая, когда учитывались все ограничения, график зависимости значения целевой функции от номера итерации приведен на рис. 4.22. В этом случае изобразить начальную точку невозможно, однако сходимость все же достигается за 13 итераций. [45]
Страницы: 1 2 3 4