Номер - координата
Cтраница 2
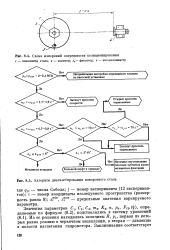 |
Схема измерений погрешности позиционирования.| Алгоритм диагностирования поворотного стола. [16] |
Соболя; j - номер эксперимента ( 12 экспериментов); i - номер координаты исследуемого пространства ( размерность равна 8); xfm, х ах - предельные значения варьируемого параметра. [17]
Таким образом, ангармоническое отношение не зависит ни от системы координат, ни от выбора номеров координат, с помощью которых оно вычисляется. [18]
Поверхность z / ( а) представляет собой гребень, склоны которого обрываются тем круче, чем больше номер координаты, по линии которой происходит спуск. [19]
Пусть на осях координат задан линейный порядок такой, что &i &2 km, где k [ - номер координаты на t - м месте порядка. [20]
Условимся обозначать точки пространства благ большими латинскими буквами, а их координаты - соответствующими маленькими буквами с индексами - номерами координат. [21]
Поэтому для нахождения соответствующей координаты напряженности магнитного поля в i, j - м узле сначала следует указать номер вектора, а затем номер координаты соответствующей компоненты. [22]
В задачах 1.87 - 1.92 написать уравнение гиперплоскости, разделяющей заданные в условиях множества MI и М & ( Размерность пространства, в котором заданы множества, совпадает с наибольшим номером координаты. [23]
В отличие от предыдущих глав мы будем в этой главе несколько иначе обозначать номера элементов матриц, а именно номер строки будем обозначать верхним, а номер столбца - нижним индексом ( dp - элемент q - й строки и р - ro столбца) и так же номер координаты элемента будем обозначать верхним индексом. Такие обозначения играют важную роль при описании тензорных величин ( см. гл. VII) и широко используются в физике. [24]
Сразу отметим, что эта таблица отличается от симплекс-таблицы для задачи (4.16) только крайним левым столбцом. Поэтому в качестве номера координаты, которую следовало бы ввести в базис на текущей итерации симплекс-алгоритма решения задачи (4.16), мы можем взять любой номер k, для которого оценка замещения о в симплекс-таблице задачи (4.15) отрицательна. [25]
Это матричное уравнение эквивалентно системе п однородных уравнений для амплитуд Asm. Первый индекс у амплитуды соответствует номеру собственной частоты, второй индекс - номеру координаты. Из системы (8.1.12) можно найти отношение амплитуд Asm / An sm - Величины Ksm образуют вектор К4, который называется вектором коэффициентов распределения амплитуд на частоте us или формой s - го собственного колебания системы. [26]
Введенная выше функция Wlfe ( tQ), играющая столь важную роль при определении вынужденных колебаний, называется частотной характеристикой системы, или, как говорят иногда, ее амплитудно-фазовой характеристикой. В зависимости от того, на какую координату действует внешняя сила и какая координата наблюдается, получаются разные частотные характеристики. Из формулы ( 67) следует, что при изменении места приложения внешней силы и номера координаты, за которой ведется наблюдение, изменяется лишь числитель дробно-рациональной функции W, знаменатель же во всех случаях одинаков. [27]
Релаксационные схемы - несомненно, солидное и заслуженное семейство, по праву гордящееся и древним происхождением, и современным преуспеянием. Однако при внешней солидности в их поведении все же кроется нечто легкомысленное. В самом деле, как они осуществляют выбор направления. Казалось бы, солидно: по порядку номеров координат. [28]
Страницы: 1 2