Номер - оболочка
Cтраница 2
В водороде имеется один электрон на s - уровне первой, / ( - оболочки, что записывается следующим образом: Is. Первая цифра означает номер оболочки, латинская буква s определяет подобо-лочку, а индекс справа - число электронов на ней. В гелии имеются два электрона, которые целиком заполняют первую оболочку. [16]
Главное квантовое число п определяет номер оболочки, к которой принадлежит электрон. Для каждого значения / возможны 2 / 1 значений т и, следовательно, различных состояний электрона. [17]
 |
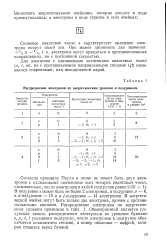
Распределение электронов при нормальной последовательности квантовых состояний. [18] |
Число электронов в слое ограничено. Электронную конфигурацию атома записывают следующим образом: первым пншут число, означающее номер оболочки, второй - букву, означающую слой, в виде показателя степени у буквы указывают число электронов в данном слое. Например, Is2, 2s2, 2p6 - это атом, который содержит два электрона в первом слое первой оболочки, два электрона в первом слое второй оболочки н шесть электронов во втором слое второй оболочки, что соответствует структуре атома неона. [19]
 |
Сравнение размеров атома и его ядра. [20] |
На каких же данных основана таблица электронных конфигураций элементов. Каждый атом теоретически имеет неограниченное число оболочек - энергетических уровней, на которых могут находиться электроны. Число, обозначающее номер оболочки, называют главным квантовым числом. Каждый электрон находится на определенном энергетическом уровне. Электроны с самым низким уровнем находятся на ближайших к ядру оболочках. Для того чтобы перевести электроны с одного уровня на другой, более высокий энергетический уровень, необходимо затратить квант энергии; наоборот, при переходе электрона на более низкий энергетический уровень испускается квант энергии. [21]
Поскольку постоянная решетки GaP известна, можно вычислить относительное число донорно-акцепторных пар для заданного расстояния R между ними, предполагая, что распределение доноров и акцепторов является случайным. На рис. 7.5 показаны расчетные распределения для спектров типов I и II в GaP. На горизонтальной шкале указаны целые числа т, соответствующие номерам оболочек для соседних пар. [23]
По законам квантовой механики электроны могут вращаться вокруг ядер не по любым орбитам. Они как бы распределяются по слоям - оболочкам. Емкость этих оболочек, максимальное число электронов в них, определяется формулой: ne2N2, где пе - число электронов, а N - номер оболочки, считая от ядра. Отсюда следует, что на первой оболочке может быть всего два электрона, на второй - восемь, на третьей - восемнадцать, на четвертой - тридцать два и так далее. [24]
 |
Распределение электронов по энергетическим уровням и подуровням. [25] |
В подуровне s может быть не более 2 электронов, в подуровне р - 6, в d - подуровне - 10 и в / - подуровне - 14 электронов. В энергетической ячейке могут быть только два электрона, причем с противоположными спинами. Общепринятой является следующая запись распределения электронов по уровням: буквами s, р, d, / указывают подгруппу, число электронов в подгруппе обозначается показателем степени, а номер оболочки - цифрой, которая ставится перед буквой. [26]
При этом применяются методы теории групп, к-рые в простейших случаях позволяют однозначно найти многочастичную волновую ф-цию ядра. С ростом номера оболочки и числа валентных нуклонов вычислит, трудности быстро растут. Но даже в тех случаях, когда точный расчет возможен, из него сложно извлечь физически важную информацию. [27]
Между законами распределения электронов по оболочкам и периодическим законом Менделеева имеется глубокая связь. Элементы нулевой группы ( инертные газы) являются элементами с полностью заполненными оболочками. Так, гелий занимает второе место в таблице Менделеева, следовательно, у него имеются два электрона, которые заполняют s - уровень в первой оболочке. Электронное строение гелия можно записать в виде Is2, где цифра 1 обозначает номер оболочки, буква s - уровень, а число электронов записывается в виде показателя степени. Начиная с атомов лития, во втором периоде идет заполнение второй оболочки, сначала s - уровня у лития и берилия и затем р-уровня - от бора до неона. Таким образом, у неона заполненными оказываются первая и вторая оболочки. [28]
Поскольку постоянная решетки GaP известна, можно вычислить относительное число донорно-акцепторных пар для заданного расстояния R между ними, предполагая, что распределение доноров и акцепторов является случайным. На рис. 7.5 показаны расчетные распределения для спектров типов I и II в GaP. На горизонтальной шкале указаны целые числа т, соответствующие номерам оболочек для соседних пар. Числа, приведенные над резкими пиками в спектре S-Si, соответствуют номерам оболочек, определенным с помощью рис. 7.5 а. Из этих рисунков видно, богатая информация содержится в спектрах ДАП. [29]
Вопрос о существовании более высоких оболочек является открытым из-за отсутствия экспериментальных данных. Из теоретических соображений следует, что оболочечные эффекты должны ослабевать с ростом массового числа. Это ослабевание обусловлено тем, что практически в любом потенциале разумной формы в оболочки группируются низшие одночастичные уровни. При возрастании порядковых номеров уровней пустые энергетические интервалы, разделяющие оболочки, становятся все более редкими и все более узкими. Все же, однако, делаются попытки предсказать магические числа ближайших высших оболочек - шестой протонной и седьмой нейтронной. Эти предсказания неоднозначны, так как с увеличением номера оболочки порядок ее заполнения становится более чувствительным к тонким деталям формы потенциала. Нетрудно изменить потенциал (3.8) так, что магическое число шестой протонной оболочки превратится в Z - 112 без изменения магических чисел известных оболочек. [30]
Страницы: 1 2 3
