Круговая номограмма

Cтраница 1

Круговая номограмма для определения глубины резко изображаемого пространства при макросъемке. [1]

Индексы окружностей круговой номограммы соответствуют тем постоянным значениям модуля А и фазы ф, при которых осуществлялось построение соответствующих окружностей. [2]

Правила работы с круговой номограммой описаны на стр. [3]

На рис. 3 - 6 приведены круговые номограммы, f позволяющие определить чистоту выделяемого 50 - 65 % - ной серной кислотой изобутилена при различной глубине извлечения его и различном содержании н-бутиленов и изобутилена в сырье. [4]

Амплитудно-частотная характеристика может быть построена по круговой номограмме ( см. рис. 5.22), которая предназначена для определения амплитудно-фазовой характеристики замкнутой системы по амплитудно-фазовой характеристике разомкнутой системы, выполняемой в координатах номограммы. [5]

Расчет ZH значительно упрощается и ускоряется, если воспользоваться графическим способом с применением круговой номограммы Вольперта-Смита. [6]

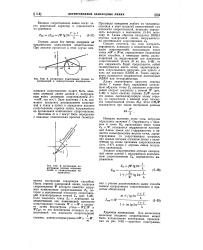К построению номограммы полных сопротивлений в прямоугольных координатах.| К построению номограммы полных сопротивлений в прямоугольных координатах. [7]

Для вычисления величины входного сопротивления может быть использована номограмма, приведенная на рис. 5 - 50, - круговая номограмма. [8]

Применение номограммы ( рис. 5.23), часто называемой номограммой для замыкания системы, основано на тех же принципах, что и применение круговой номограммы. В координатах номограммы строится амплитудно-фазовая характеристика разомкнутой системы и затем по точкам пересечения ее с кривыми номограммы определяются логарифмические амплитудная и фазовая характеристики замкнутой системы. Полагаем для примера, что построенная характеристика имеет вид кривой, выполненной штриховой линией. Пусть точка В на амплитудно-фазовой характеристике соответствует частоте to - и через эту точку проходят две кривые номограммы. [9]

Тогда нижняя часть ОВА построенных окружностей, расположенная под осью абсцисс, будет соответствовать отрицательной фазе if указанного диапазона. Обычно на круговых номограммах около окружностей, расположенных над осью абсцисс, проставляется положительная фаза. [10]

На прилагаемой к этой книге вкладке напечатаны два диска описанной номограммы. Читатель может, вырезав диски, сделать себе круговую номограмму и пользоваться ею в своей практической работе. [11]

Для определения глубины резко изображаемого пространства можно построить номограмму и пользоваться ею. Очень удобна номограмма с круговой шкалой, изображенная на рис. 4, дающая возможность определять глубину резкости для различных по величине диаметров кружка рассеяния. Круговая номограмма состоит из двух дисков. [12]

Страницы: 1