Нуль - замкнутая система
Cтраница 1
Нули замкнутой системы являются нулями. [1]
В следующем разделе рассмотрено наличие и распределение полюсов и нулей различных замкнутых систем и регуляторов. Это же сделано и для регуляторов состояния. Поскольку обобщенные линейные регуляторы допускают большую свободу в задании полюсов, по крайней мере по сравнению с другими регуляторами входа / / выхода, описанными здесь, они рассмотрены первыми. [2]
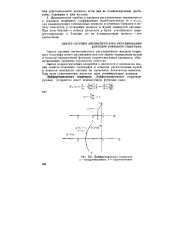 |
Дифференциальная коррекция. о - некорректированная. б - корректированная. [3] |
Динамическая ошибка в процессе регулирования определяется в основном величиной коэффициента колебательности т а / для доминирующих комплексных полюсов и степенью близости к началу плоскости р остальных полюсов и нулей замкнутой системы. При этом близкие к началу плоскости р нули увеличивают перерегулирование, а близкие, но не доминирующие полюсы - его уменьшают. [4]
В передаточных функциях Gw ( z) или Gn ( z) полюса полиномов A ( z) zd или А0 ( z) zd всегда компенсируются соответствующими нулями. Нули замкнутой системы определяются нулями объекта только для задающего входного сигнала. [5]
Поскольку при проектировании систем управления почти всегда следует учитывать изменения параметров объекта, в гл. Оцениваются расположение полюсов и нулей замкнутых систем, качество процессов и затраты на управление. Исследование свойств алгоритмов завершается приведением рекомендаций по их использованию. [6]
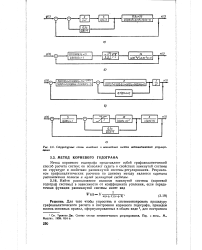 |
Структурные схемы линейных и нелинейных систем автоматического регулирования. [7] |
Метод корневого годографа представляет собой графоаналитический способ расчета систем; он позволяет судить о свойствах замкнутой системы по структуре и свойствам разомкнутой системы регулирования. Результатом графоаналитических расчетов по данному методу является картина расположения полюсов и нулей замкнутой системы. [8]
Как видно из уравнения (2.12), нули передаточной функции замкнутой системы имеют место при F, стремящемся к бесконечности ( полюса F), и при G, обращающемся в нуль. Вполне воз-можио, что полюс замкнутой системы окажется вблизи нуля G, который является также нулем замкнутой системы. [9]
Траектории полюсов заканчиваются в точке расположения нулей передаточной функции разомкнутой системы Gz. Когда коэффициент усиления К приближается к бесконечности, передаточная функция приближается к единице вследствие того, что полюса ( являющиеся корнями i - - KG) приближаются к Gz. Нули замкнутой системы всегда совмещены с нулями Gz. [10]
Линии 180 функции KG являются геометрическим местом полюсов передаточной функции замкнутой системы при отрицательной единичной обратной связи. Истинным местоположением полюсов при заданных конкретных условиях являются точки перенесения линии 180 функции G с линиями амплитуды 1 / К. Нули замкнутой системы совпадают с нулями G. [11]
На рис. 4.2 а приведена характеристика самого самолета на s - плоскости. Четыре полюса замкнутой системы / расположены на линиях 0, выходящих из четырех полюсов разомкнутой системы X. Нулями замкнутой системы Г ] являются два полюса разомкнутого контура А, расположенные на вещественной оси. Можно видеть, что самолет без системы управления слабо демпфирован и обладает длиннопериодическими фугоидными колебаниями, возникающими при воздействии случайных вертикальных сил. [13]
Положение полюсов и нулей передаточной функции разомкнутой системы в s - плоскости можно найти графически. Линии усиления и фаз можно начертить по следующим правилам: фаза равна сумме углов от всех нулей минус сумма углов от всех полюсов, а коэффициент усиления равен произведению расстояний до всех нулей, разделенному на произведение расстояний до всех полюсов. Полюса замкнутой системы находятся на пересечениях фазовых линий 180 и линий 0 дб в диаграмме разомкнутой системы. Нули замкнутой системы являются нулями передаточной функции прямой цепи и полюсами передаточной функции цепи обратной связи. [14]
Страницы: 1
