Анализ - фазовая диаграмма
Cтраница 1
Анализ фазовых диаграмм показывает, что в области составов промышленных сплавов Fe-Ni-Al ( u y) превращение отсутствует. [1]
Анализ фазовых диаграмм показывает, что появление так называемых фракций переменного состава и временное снижение температуры дистиллята связано не с существованием криволинейных разделяющих линий и переходом процесса из одной области в другую, а с существованием точек перегиба на линиях периодической ректификации. В соответствии с этим, эффекты падения температуры дистиллята и зигзагообразного хода линий дистиллята могут наблюдаться и в тех системах, где они не могут быть объяснены или предсказаны исходя из существующей концепции, например, в системах без азеотропов, что подтверждено нами экспериментально. [2]
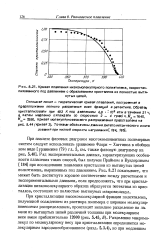 |
Кривая плавления низкомолекулярного полиэтилена, закристаллизованного под давлением с образованием кристаллов из полностью вытянутых цепей. [3] |
При анализе фазовых диаграмм многокомпонентных полимерных систем следует использовать уравнение Флори - Хаггинса в обобщен ном виде [ уравнение ( 79) гл. Ряд экспериментальных данных, характеризующих особенности плавления таких смесей, был получен Праймом и Вундерлихом [ 184] при исследовании плавления кристаллов из вытянутых цепей полиэтилена, выращенных под давлением. [4]
Однако при анализе фазовых диаграмм таких систем возникают некоторые осложнения. Трудно, например, получить значение температуры плавления чистого ненабухшего полимера. Существует также вероятность того, что растворитель может войти в кристаллическую решетку и стать составной частью кристаллографической структуры. Например, поглощение воды коллагеном и нуклеиновыми кислотами сопровождается усилением экваториальных рентгеновских рефлексов [14, 15], что указывает на проникновение растворителя в упорядоченную фазу. При этих обстоятельствах условия равновесия, определяемые соотношением ( 10), уже не достаточны, и должны быть выполнены некоторые дополнительные требования. [5]
Аналогичный подход к анализу тройных и многокомпонентных фазовых диаграмм слишком длинен для того, чтобы его можно было осветить на страницах данной книги. Однако введение в такой анализ явно полезно и поэтому рассмотрим его в разделах 10.1 и 10.2. Для более глубокого изучения читателю следует обратиться к ссылкам [1-4], в которых прекрасно изложен этот материал. В 10.3 мы рассмотрим возможные формы аналитического представления энергии Гиббса многокомпонентной фазы, а в 10.4 - способы расчета многокомпонентной фазовой диаграммы. [6]
Излагаются основные результаты работ по анализу фазовых диаграмм открытой дистилляции и периодической ректификации: приводится уравнение линии пара при равновесном дистилляции, сформулировано условие существования точек перегиба на дистилля-ционных линиях, уточнено понятие областей дистилляции. [7]
Все эти параметры определяются на основе анализа фазовых диаграмм и возможных фазовых переходов в системе. [8]
Решение задачи в термодинамическом аспекте проводится на основе анализа фазовых диаграмм. [9]
Следует сказать, что эти формулировки устойчивости в малом эффективны для линейных систем, для нелинейных же дело обстоит сложнее, как это можно видеть из анализа первых фазовых диаграмм для нашего частного примера и как мы убедимся впоследствии. [10]
Как показано в последующих главах, обоснованный выбор схемы процесса, определение скоростей, при которых будет протекать экстракция, оптимальное объемное соотношение экстрагента и исходного раствора, а также выяснение изменения концентраций фаз при экстракции возможны лишь на основе анализа фазовых диаграмм равновесия. В связи с тем, что подробно исследовано сравнительно немного трех-компонентных систем и еще меньшее число четырехкомпонентных, обычно возникает необходимость в экспериментальном определении равновесия для новых экстракционных процессов. [11]
Обнаружены две области трехфазного равновесия жидкость - жидкость - газ. Проведен анализ фазовой диаграммы в данной системе. [12]
Следует заметить, что целесообразность выбора способа выражения состава в аналитических или истинных мольных долях определяется характером рассматриваемой задачи. Так, при анализе фазовых диаграмм пар - жидкость и исследовании условий фазовых превращений целесообразность выражения состава пара в аналитических мольных долях не вызывает сомнений. [13]
В качестве исходных данных используются давление и температура в верхней части десорбера. Таким образом, оценка потерь ДЭГа в виде пара может быть выполнена на основе анализа фазовых диаграмм жидкость - пар системы ДЭГ - вода. [14]
В разделе 3.2 мы рассмотрим равновесия, стабильные относительно всевозможных видов флуктуации, имеющих бесконечно малую величину. Изучение стабильности относительно больших флуктуации несколько отличается, так как в данном случае нет ограничений, которые нужно учитывать при изучении локальных положений; мы встретимся с ними при анализе фазовых диаграмм. В разделе 3.3 будут выведены критерии стабильности по отношению к малым флуктуациям состава в бинарных растворах, эти критерии будут использованы в четвертом разделе при определении спинодали и критической точки. Ее применение рассмотрено в гл. И, наконец, в 3.6 для иллюстрации разработанных в этой главе принципов мы оценим изменение свободной энергии, связанное с зарождением и ростом включений. [15]
Страницы: 1 2