Анализ - дисперсия
Cтраница 1
 |
Анализ дисперсий. [1] |
Анализ дисперсий включает раздельно все поддающиеся определению факторы, входящие в общую сумму квадратов. Сумма квадратов, обусловленная отклонением средней величины, обычно велика по сравнению с суммой квадратов, определяющейся всеми другими участвующими факторами. Эти прочие компоненты и дают величину общего отклонения от средней величины. [2]
 |
Дополненная факторная схема проведения экспериментов. эта схема дает точки, необходимые для согласования с моделирующим уравнением второго порядка. [3] |
Анализ дисперсий для этого эксперимента обнаруживает лишь незначительное несогласие. Сумма квадратов, обусловленная регрессией, весьма значительна. Следовательно, в этом новом интервале условий эксперимента моделирующее уравнение хорошо согласуется с опытными данными. [4]
Анализ дисперсии позволил заключить, что на уровне значимости р 0 05 перечисленные факторы не оказывают влияния на данные показатели фармакокинетики исследованных препаратов. [5]
Анализ дисперсии оптического вращения полипептидов и белков. Анализ дисперсии оптического вращения полипептидов и белков. Анализ дисперсии оптического вращения полипептидов и белков. Анализ дисперсии оптического вращения полипептидов и белков. [6]
Анализ дисперсии оптического вращения полипептидов и белков. [7]
Проведем анализ дисперсии в экранированной НПЛ на ферромагнитной подложке ( рис. 1.31, а), намагниченной касательно и поперечно по отношению к направлению распространения энергии. [8]
 |
Хроматограмма маточного раствора от производства поливинил-кета ля. [9] |
При анализе дисперсий на содержание остаточного мономера - винилбутилового эфира необходимо учитывать, что последний в водных средах может гидролизоваться. Поэтому определение его в сополимернои дисперсии нужно проводить сразу же после получения дисперсии. [10]
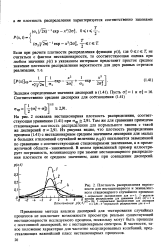 |
Плотность распределения вероятности для нестационарного и эквивалентного стационарного случайного процесса. [11] |
Применение метода анализа дисперсий для тестирования случайных процессов не исключает возможности просмотра реально существующей нестационарности исследуемого процесса, поскольку могут быть процессы с постоянной дисперсией, но с нестационарным спектром. В частности, такое положение характерно для частотно модулированных колебаний, представляющих важнейший класс нестационарных процессов. [12]
 |
Расчет дисперсии начальной механической скорости проходки. [13] |
В то же время анализ дисперсий с помощью критерия Фишера [1] показал, что обе модели адекватны реальному процессу при 10 % - ном уровне значимости. Следовательно, обе эти модели могут применяться для прогнозирования показателей работы долот в данных условиях. [14]
Непосредственному расчету / - критерия предшествует анализ дисперсии. [15]
Страницы: 1 2 3