Анализ - конкретная задача
Cтраница 1
Анализ конкретных задач, возникающих на различных этапах проектирования, приводит к следующему выводу. Многие задачи обработки информации, планирования и управления в АСУ представляют собой непрерывные экстремальные задачи. [1]
При анализе конкретных задач будут употребляться также средние по if значения аз, Рз, з и некоторых их комбинаций, выписанные ниже. [2]
При анализе конкретных задач становятся возможными различные упрощения. Частные формы записи системы дифференциальных уравнений тепломассообмена приведены в соответствующих параграфах этой главы. [3]
При анализе конкретных задач течения жидкостей в трубопроводах или в технологических аппаратах часто рассматриваются некоторые частные случаи. Значительно упрощается система уравнений (1.29) для потоков так называемой идеальной жидкости, не обладающей свойством вязкого трения ( ц О, v 0); для такой жидкости равны нулю последние слагаемые правых частей уравнений (1.29), что понижает порядок дифференциальных уравнений со второго до первого, но не ликвидирует нелинейность этих уравнений. С некоторым допущением идеальными жидкостями ( не путать с принятым в молекулярно-кинетической теории газов понятием идеального газа, который обладает свойством вязкого трения) можно полагать, например, разреженные газы, обладающие малыми значениями коэффициентов вязкого трения, на течение которых силы вязкого трения практически не оказывают влияния по сравнению с другими силами. К сожалению, и упрощенные уравнения движения идеальной жидкости ( так называемые уравнения Эйлера) могут быть аналитически решены также лишь в самых простых случаях, далеко не исчерпывающих практические задачи гидромеханики. [4]
Очевидно, что для анализа конкретной задачи массового обслуживания необходимо располагать информацией по длительности обслуживания клиентов. [5]
Цг, Цп при анализе конкретных задач должны быть известны из технико-экономической справочной литературы и при нахождении минимума 773 фигурируют в качестве известных параметров. [6]
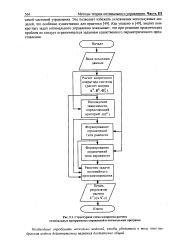 |
Структурная схема алгоритма расчета оптимальных программных управлений и оптимальных программ. [7] |
Как указано в [49], анализ конкретных задач оптимального управления показывает, что при решении практических проблем не следует ограничиваться заданием единственного параметрического представления. [8]
Типовые работы формируют на основе анализа конкретных задач, которые предстоит решать на ЭВМ в АСУ. [9]
Они должны быть заданы независимо при анализе конкретной задачи. Так, например, при конвективной сушке, как правило, используются условия третьего рода. Интенсивный обдув теплоносителем ( Bi 52 20) обеспечивает предельный случай, когда условия третьего рода переходят в условия первого рода и потенциалы переноса в окружающей среде и на поверхности материала становятся практически равными. [10]
Наибольшие сложности в применении принципа сжатых отображений к анализу конкретных задач обычно заключаются в проверке справедливости условия Липшица с соответствующим коэффициентом. [11]
В следующих двух разделах мы покажем, как используется этот метод при анализе конкретных задач о дисперсионном волновом движении. Если величина т такова, что существуют действительные точки стационарной фазы, удовлетворяющие соотношению m C ( k), TO решение ( 28) становится эквивалентным результату ( 21), полученному методом стационарной фазы. С другой стороны, и это - главное преимущество метода седло-вой точки, в случаях, когда в уравнении C ( k) т нет действительных корней, выражение ( 28) непосредственно дает экспоненциально убывающий сигнал, о котором уже упоминалось ранее. [12]
В § 3.4 будет показано, что формула (3.31), полученная здесь путем анализа конкретной задачи, является общей для любых сил, действующих на материальную точку. [13]
Использование принципа излучения в такой форме, естественно, затруднено, однако, как следует из анализа конкретных задач, трудно надеяться на возможность более простой формулировки условий однозначности. Трудности математического характера, возникающие при постановке граничных задач теории упругости, отражают сложность физического процесса распространения упругих волн. [14]
Теория электромагнитного поля изучается на базе векторного анализа, позволяющего в наиболее краткой форме производить выводы и доказательства, а анализ конкретной задачи сводится к отысканию решений дифференциальных уравнений, записанных в наиболее подходящей для этой задачи системе координат. [15]
Страницы: 1 2 3