Анализ - заселенность
Cтраница 1
Анализ заселенностей ( см. табл. 11.2) показывает, что, как и следовало ожидать, при образовании связи В-N происходит перенос ст-электронной плотности ( главным образом 2ра) с атома азота. Это сопровождается возрастанием заселенности 2рчг - орбиталей азота, компенсирующим указанный выше 7-зффект, что приводит к небольшому результирующему повышению атомной заселенности азота. Очень небольшие различия между энергиями связи F ( ls) следуют ходу изменения ПИ бора и также коррелируют с изменениями зарядов атомов фтора, несмотря на то что последние тоже невелики. [1]
Анализ заселенностей для молекулы СН4 проведен не был. [2]
Анализ заселенностей NiF64 в первом возбужденном состоянии 3T2g показывает, что при возбуждении 3Л2й - 3Г2в происходит перенос примерно 0 02 е от металла к лигандам. [3]
Как показал анализ энергетических заселенностей нормальных мод, описанная процедура задания начальных условий приводит к равномерному распределению колебательной энергии молекулы по нормальным модам. [4]
В таких случаях анализ заселенностей должен был привести к отнесению всего электронного заряда молекулы к одному атому, ядро которого выбрано в качестве начала отсчета при разложении волновых функций. Однако анализ заселенностей приводит к физически правильным результатам, если базис атомных орбиталей выбран в соответствии с электронным строением атомов, образующих рассматриваемую молекулу. [5]
В последнее время анализ заселенностей Малликена критикуется в литературе как за плохо обоснованное для орбиталей с разной пространственной локализацией деление поровну заселенности перекрывания, так и за то, что электронный заряд, определяемый диагональными элементами матрицы плотности Ряя, полностью приписывается атому А, хотя некоторая доля его расположена в области других атомов. [6]
Согласно этим утверждениям, анализ заселенности можно использовать для определения валентных углов, если соответствующие молекулярные орбитали включают гибридные з / Аорби-тали центрального атома. Мы проведем обсуждение этого вопроса, полагая, что в данном случае справедливы выведенные Коулсоном 13 ] условия ортогональности. [7]
Для кристаллов можно использовать и анализ заселенностей (3.24), что, по-видимому, как и для молекул, целесообразно в тех случаях, когда в атомном базисе содержатся орбитали возбужденных состояний атомов. [8]
Однако несмотря на эти недостатки, малликеновский анализ заселенностей очень хорошо прижился в современной квантовой химии. [9]
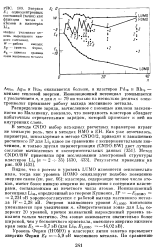 |
Энергия EI однозлектронвых состояний ( точки как функция числа п атомов в кластерах Lin. [10] |
Распределение заряда, вычисленное с помощью анализа заселенности по Малликену, показало, что поверхность кластеров обладает избыточным отрицательным зарядом, который притекает к ней из внутренних слоев. [11]
Из трех упоминавшихся в § 3.2. схем анализа заселенностей наиболее последовательной в случае кристаллов ( в том числе и в расчетах электронных состояний по методу КРЭЯ) представляется схема левдинского анализа заселенностей, связанная с переходом к симметрично-ортогонализованному базису и не приводящая к явной зависимости зарядов на атомах от решеточных интегралов перекрывания. В связи с этим заметим, что на основе симметричной ортогонализащш функций отдельных ионов Левдин развил последовательную квантовомехани-ческую теорию для вычисления энергии связи в щелочно-гало-идных кристаллах, результаты которой хорошо согласуются с данными эксперимента. [12]
В связи с этим предложен ряд усовершенствованных схем анализа заселенности, однако до сих пор они не получили сколько-нибудь широкого распространения. [13]
Петере [977] использовал полученные Капланом и Дунканом волновые функции для анализа заселенностей. В табл. 44 приведены коэффициенты перед атомными орбиталями [ см. равенства ( 111 12) ], вычисленные Капланом, а в табл. 45 - парные заселенности, полученные на их основе Петерсом. [14]
Анализ распределения электронов в терминах заселения ими атомных орбиталей называют анализом заселенностей. [15]
Страницы: 1 2 3 4