Область - пластичность
Cтраница 2
В последнее время мы уцепились за одну идею в области пластичности, где можно, пожалуй, построить количественную leopmo, по я не мог бы сделать этого раньше, потому что соответствующие экспериментальные факты не были установлены и основ для теории не существовало. [16]
Можно было бы привести очень много примеров различных явлений из области пластичности и прочности кристаллов, которые мы или не можем пока совсем объяснить, или даем только качественное объяснение. [17]
Пусть бп К, ) Q I к 0 - область пластичности решения и 2У - Q Qn - область упругости. [18]
В общем случае при деформировании совместным растяжением и изгибом сначала появляется одна область пластичности вблизи кромки / или 2 ( рис. 29), затем две области пластичности, сливающиеся при дальнейшем деформировании, так что все сечение оказывается пластичным, Однако этот третий этап не всегда реализуется. [19]
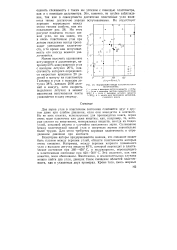 |
Корреляция между пластичностью и вспучиванием. [20] |
Некоторые авторы придерживаются мнения, что спекание может быть плохим между зернами углей, области пластичности которых очень смещены. Например, между зернами жирного пламенного угля с выходом летучих веществ 40 %, который переходит в пластическое состояние при 360 - 450 С, и полужирного, переходящего в пластическое состояние при 420 - 500 С. Эти опасения, как нам кажется, мало обоснованы. Фактически, в исключительных случаях можно найти два угля, дающих такое смещение областей пластичности, как в указанных двух примерах. [21]
Новые трудности оказываются перед нами, как только мы достигаем предела упругости и вступаем в область пластичности. [22]
Новые трудности оказываются перед нами, как только мы достигаем предела упругости и вступаем в область пластичности. [23]
Другой путь решения упруго-пластических плоских задач применяется для тел, материал которых не обладает упрочнением в области пластичности применяется метод характеристик и разыскивается граница сопряжения области пластичности с упругой областью. Кинематические и статические условия сопряжения вследствие гипотезы несжимаемости в первой из этих областей не всегда совместны, но иногда достаточно пользоваться только статическими условиями. Надо иметь в виду, что в задачах о концентрации для материалов без упрочнения важно знать не столько распределение напряжений ( поскольку интенсивность их заведомо постоянна), сколько распределение деформаций, по которым можно судить об опасности разрушения. В задачах о несущей способности, конечно, достаточно найти распределение напряжений, и рассматриваемый метод ведет к цели. Необходимо отметить успешное решение ряда задач о плоском напряженном состоянии. [24]
В программе учтены зависимость динамических напряжений от скорости пластической деформации, линейное деформационное упрочнение, распространение вдоль пролета областей пластичности и упрочнения. Решение системы уравнений выполняется методом Рунге-Кутта четвертого порядка. Программа позволяет выяснить резервы прочности балок за счет их приспособляемости к динамической нагрузке. [25]
 |
Зависимость растяжения ст. в волокне от длины волокна средних напряжений. IJd. [26] |
Согласно Келли и Тайсону, в окрестностях концов волокна, где действуют большие напряжения сдвига на поверхности раздела, появляются области пластичности и величина тт принимает постоянное значение. [27]
При разных знаках деформаций возможны четыре варианта областей пластичности: одна область со стороны большого или малого радиуса бруса, две области пластичности и целиком пластическое сечение. [28]
Известные методы формования волокон также неприменимы для производства волокна из фторсодержащих полимеров вследствие неплавкости и нерастворимости полимера, а также отсутствия области пластичности. Волокно тефлон формуется по принципиально новому методу, основанному на использовании водных коллоидных дисперсий полимера и полученных из них паст и органозолей, что также удорожает процесс. [29]
Теория пластичности устанавливает связь между напряжениями и деформациями ( деформационные теории ] или скоростями изменения деформаций ( теории пластического течения) в областях пластичности материалов. При этом часто напряжения зависят не только от текущих деформаций, но и от истории ( процесса) деформирования. Естественно, что соответствующие задачи в силу нелинейной связи напряжений с деформациями оказываются гораздо сложнее задач теории упругости. [30]
Страницы: 1 2 3 4