Область - решение - система
Cтраница 2
IV, § 6 ( Вывод) известно, что областью решений системы ( 26) является некоторый выпуклый многогранник в рассматриваемом пространстве. [16]
Определение значений силы П и углов 0, при которых возможно существование формы с двумя точками перегиба, позволит ограничить область решений системы ( 11) - ( 13) с условиями ( 20) - ( 25) и составить наиболее удачный алгоритм. [17]
Штриховка показывает те из полуплоскостей, которые являются областями решений соответствующих неравенств. Областью решений системы неравенств является выпуклый четырехугольник. [18]
Штриховка показывает те из полуплоскостей, которые служат областями решения соответствующих неравенств. Областью решений системы неравенств является выпуклый четырехугольник. [19]
Штриховка показывает те из полуплоскостей, которые служат областями решений соответствующих неравенств. Областью решений системы неравенств является выпуклый четырехугольник. [20]
Система условий, состоящая из уравнений и неравенств, содержащих неизвестные х и у или только какую-нибудь одну из этих величин, называется смешанной системой. Введем понятие области решений системы, относящееся как к смешанным системам, так и к системам, состоящим только из уравнений или только из неравенств с двумя неизвестными. [21]
Графическое решение этой задачи показано на рис. 12 слева. При построении области решений системы неравенств следует учесть, что переменные у и ( / 2 могут принимать как положительные, так и отрицательные значения. [22]
О 4), следовательно, соответствующая полуплоскость располагается по отношению к граничной прямой ( 3) по другую сторону, нежели начало координат. Очевидно, областью решения системы трех неравенств служит треугольник, ограниченный данными тремя граничными прямыми, с вершинами, являющимися точками пересечения этих прямых. Для нахождения их координат нужно решить совместно соответствующие пас уравнений. [23]
Вообще, если среди условий какой-нибудь системы содержится условие ( уравнение или неравенство), область решений которого пуста, то независимо от того, каковы остальные условия этой системы, можно утверждать, что область ее решений пуста. Однако обратное утверждение неверно: область решений системы может оказаться пустой и в том случае, если области решений, соответствующие каждому из ее условий, не пусты. [24]
Совокупность всех этих точек и есть искомое множество решений рассматриваемой системы. На рис. 63 части гиперболы, составляющие область решений системы, выделены жирной линией. [25]
Для отыскания области решений произвольной смешанной системы сначала нужно рассмотреть каждое из ее условий ( каждое уравнение и каждое неравенство) в отдельности и найти на плоскости хОу множество всех тех: точек координаты каждой из которых этому условию удовлетворяют. Если область решений системы содержит хотя бы одну точку, систему называют совместной. [26]
Так как из 1-го неравенства 2 2 i, то отсюда следует, что и вторая переменная ограничена. Как видно из рисунка, рассматриваемая область неограничена снизу. Наконец, область решений системы ( 3) ограничена снизу, но неограничена сверху. Таким образом, обе переменные ограничены снизу. [27]
Это пересечение образует какое-то многогранное тело. В силу выполнения неравенств ( точки по одну сторону от каждой плоскости) это тело обязательно выпукло. В итоге делаем вывод: областью решений системы линейных неравенств с тремя переменными является выпуклый многогранник IB пространстве, ограниченный соответствующими плоскостями. Некоторая часть каждой такой плоскости образует грань, пересечение двух граней дает ребро, а трех - вершину многогранника. [28]
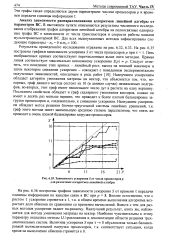 |
Зависимость ускорения S от числа процессоров / для различных алгоритмов линейной алгебры. [29] |
Вполне естественно, что с ростом т ускорение стремится к 1, т.к. в общем времени выполнения алгоритма возрастает доля обменов по сравнению со временем вычислений. Вместе с тем для разных методов ускорение падает по-разному. Наилучший результат, опять же, наблюдается для метода умножения матрицы на вектор. Наиболее чувствительны к этому параметру оказались методы LU-разложения и декомпозиции области решения трех-диагональных систем. [30]
Страницы: 1 2 3