Область - допустимое решение - задача
Cтраница 1
Область допустимых решений задачи (1.4) - (1.5) образуется пересечением т множеств. [1]
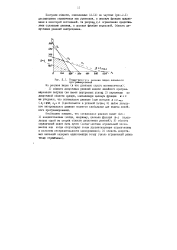 |
Геометрическое решение задач линейного программирования. [2] |
I) область допустимых решений задачи линейного программирования выпукла ( не имеет внутренних углов); 2) перемещая по допустимой области прямую, описывающую целевую функцию щ с. Xj о)) достигается в угловой точке; 3) любое локальное экстремальное решение является глобальным для задачи линейного программирования. [3]
На рис. 17 построена область допустимых решений задачи Р0 и показано определение ее оптимального решения. [4]
Точка Я ( 3) не принадлежит области допустимых решений задачи. [5]
Проверим теперь, принадлежит ли эта точка области допустимых решений задачи. Так как g ( Xl) 0, то X1 принадлежит области допустимых решений. [6]
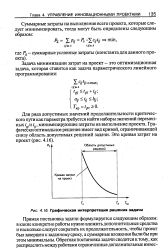 |
Графическая интерпретация решения задачи. [7] |
Графически оптимальное решение имеет вид кривой, ограничивающей снизу область допустимых решений задачи. [8]
Пересечение указанных полупространств является многогранником, который и будет областью допустимых решений задачи. [9]
Совокупность всевозможных допустимых решений ( планов) задачи называют областью допустимых решений задачи. [10]
В евклидовом пространстве Еп система ограничений ( 2) определяет область допустимых решений задачи. В отличие от задачи линейного программирования она не всегда является выпуклой. [11]
Так как точка Х ( 6, 7) принадлежит области допустимых решений задачи, то второе слагаемое в квадратных скобках формулы ( 72) равно нулю. [12]
Находят по всем переменным частные производные от целевой функции и функций, определяющих область допустимых решений задачи. [13]
К первой группе относятся методы, при использовании которых исследуемые точки не выходят за пределы области допустимых решений задачи. Наиболее распространенным из таких методов является метод Франка - Вулфа. [14]
В том случае, если в задаче линейного программирования две переменные х и х2 и область допустимых решений ограничена, оптимальное решение может быть получено путем параллельного перемещения параметрического семейства прямых c ] x ] c2x2d до пересечения с областью допустимых решений задачи. [15]
Страницы: 1 2