Область - сечение
Cтраница 1
 |
Зависимость изгибающего момента от кривизны при als ( 0 0 2. В - Л ( 0. я 0 2. [1] |
Область сечения, находящаяся в упругом состоянии, оказывает заметное влияние на Мг только при относительно малой кривизне гибки. [2]
В области втулочных сечений за рабочим колесом осевая составляющая абсолютной скорости изменяет направление, что приводит к наличию обратных течений. Возникает кольцевой вихрь, опоясывающий втулку рабочего колеса и распространяющийся на область отсасывающей трубы. [3]
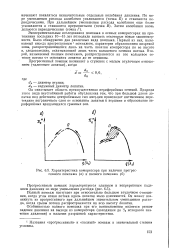 |
Характеристика компрессора при наличии прогрессивного помпажа ( а и полного помпажа ( б. [4] |
Он охватывает область преимущественно периферийных сечений. Природа-этого вида неустойчивой работы обусловлена тем, что при большой длине лопатки под действием центробежных сил инерции происходит интенсивное перетекание пограничного слоя от основания лопатки к вершине и образование периферийных вращающихся срывных зон. [5]
На контуре области сечения функция напряжений принимает значение, равное нулю. [6]
 |
Схема определения эквивалентного канала методами статических мо. [7] |
В случае скопления каналов в одной области сечений или прохождения одного канала достигается практически абсолютная сходимость, что позволяет рекомендовать метод суперпозиции для определения обобщенного канала. [8]
 |
Схема распределения напряжений в упругой области в образце с круговой выточкой при изгибе. [9] |
А - площадь минимального сечения; Лупр - область сечения образца, которая деформируется упруго; Апл - область сечения образца, которая деформируется пластически. [10]
Требуется определить: 1) границу между упругой и пластической областями сечения ( са); 2) построить эпюру нормальных напряжений о; 3) определить остаточные напряжения после разгрузки и построить эпюру остаточных напряжений Оост. [11]
Требуется определить: 1) границу между упругой и пластической областями сечения ( со); 2) построить эпюру нормальных напряжений о; 3) определить остаточные напряжения после разгрузки и построить эпюру остаточных напряжений оо; 4) определить остаточную кривизну оси бруса и величину остаточного прогиба в его середине. [12]
Следовательно, задача о кручении стержня сводится к определению гармонической в области сечения стержня функции, когда на контуре сечения задано значение нормальной производной этой функции. [13]
Отметим, что при точном решении задач по кручению прокатных профилей области сечений были взяты без закруглений около соединений стенок профиля с полками. Следовательно в табл. 2 в данных приближенных формулах для прокатных профилей не учтены влияния закруглений в областях соединений стенок профиля с полками. Однако имеющиеся закругления могут оказать влияние на величину жесткости прокатного профиля в сторону ее незначительного увеличения. Закругления в значительной мере ослабляют местную концентрацию напряжений у входящих углов профиля. Величина же максимального напряжения, приведенная в табл. 2 для данного профиля, не получит ощутительного изменения, если это напряжение возникает в точке в достаточном удалении от входящего угла. [14]
Из уравнения ( 1) следует, что наибольшие сдвиги имеют место в той области сечения витков, точкам, которой соответствуют относительно большие радиусы-векторы р и малые значения координат и. В этой области при заневоливании имеют место пластические деформации. Для остальной части сечения материал виг-ков деформируется упруго. [15]
Страницы: 1 2 3