Черная область

Cтраница 3

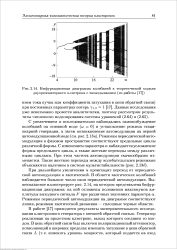Бифуркационная диаграмма колебаний в теоретической модели двухрезонаторного клистрона с запаздыванием ( из работы. [31]

При дальнейшем увеличении а происходит переход от периодической автомодуляции к хаотической. В области хаотических колебаний наблюдается большое число окон периодической автомодуляции. Вышесказанное иллюстрирует рис. 2.14, на котором представлена бифуркационная диаграмма: на ней отложены положения максимумов амплитуды выходного сигнала F при различных значениях параметра а. Режимам периодической автомодуляции на диаграмме соответствуют линии, режимам хаотической динамики - сплошные черные области. [32]

На листе коричневой бумаги рисуется карта. У L-черная краска, у R-белая. Игроки поочередно закрашивают области на карте, следя за тем, чтобы области, примыкающие друг к другу вдоль линейного участка границы, не были окрашены в один цвет. Полезно мысленно представить все области, примыкающие к белой области, окрашенными в белый цвет, а все области, примыкающие к черной области, окрашенными в черный цвет. Тогда все области, которые должны быть окрашены и в белый, и в черный цвета, следует изъять с карты как не поддающиеся правильному раскрашиванию. [33]

Свсрхскопления галактик имеют большие размеры ( 20 - 100 Л 1 Мпк, по концентрация галактик в них существенно меньше. Они, как правило, сильно анизо-трошш ( отношение осей до 1: 10), состоят из неск. Выделено около десятка сверхскоплений, среди к-рых есть сплюснутые, как Местное сверхскопление, в к-ром расположена наша Галактика, и вытянутые, как сверхскоиление в созвездиях Персея - Рыб. Сверхскопления не обладают четкими границами, они непрерывно переходят одно в другое, образуя единую связную структуру, к-рую паз. Между сверхскоплениями обнаружены гигантские черные области, достигающие 100 / s 1 Мпк в поперечнике, в к-рых галактики практически отсутствуют. Мпк, Вселенная практически однородна. [34]

Диаграмма ориентированного зацепления используется для построения его поверхности Зейферта. Диаграмма D распадается на такие окружности Зейферта С j, причем они могут лишь соприкасаться. Для каждой двойной точки а - рассматривается прямоугольник / / -, помещенный вертикально над а -, к-рый скручивается на 90 так, чтобы верхняя сторона лежала на крае D jt, а нижняя - на крае В / а, если Сjl и Суа - примыкающие к а - окружности Зейферта. Так получаемая поверхность ориентируема. Более простую, но, возможно, неориентируемую поверхность, натянутую на зацепление, можно построить, взяв цо диску над каждой черной областью шахматной диаграммы и соединив их, как и выше, скрученными прямоугольниками. [35]

Страницы: 1 2 3