Подобная область
Cтраница 1
 |
Схемы расположения макромолекул и диполей в полимере до поляризации ( а и после нее ( б. [1] |
Подобная область диэлектрических потерь появляется в ПК после ориентационной вытяжки. [2]
Причем подобные области в отношении избранной системы координат располагаем так, что они могут быть совмещены путем изменения линейных размеров одной из них в kt раз. [3]
Существование подобных областей D ( ЗСЛ ( при л 1) вытекает из доказываемой ниже теоремы. [4]
Для образования подобных областей используются различные технологические процессы. Все они сводятся к созданию взаимосвязанного расположения электронных элементов в соответствии с теми функциями, которые должна выполнять схема. [5]
Для образования подобных областей используются раз - личные технологические процессы. Все они сводятся к созданию взаимосвязанного расположения электронных элементов в соответствии с теми функциями, которые должна выполнять схема. Рассмотрим основные виды интегральных микросхем. [6]
Хотя для подобных областей применения можно использовать как обычные материалы, так и материалы с улучшенными свойствами, однако совершенно очевидно, что ограничение диффузии солей к стальному каркасу железобетона является очень важным, поскольку позволяет увеличить срок службы изделий. В работе [614] также установлено, что импрегниро-вание полимерами снижает коррозию стального каркаса даже в бетонах с высоким содержанием солей. Как показано на рис. 11.17, в импрегнированном железобетоне, содержащем соли, коррозии стальных элементов не наблюдается после циклических испытаний нагрев - охлаждение, в то время как в контрольных образцах обнаружены значительные очаги коррозии. [8]
При математизировании любой подобной области трудность может быть обойдена путем создания аксиоматики, но тогда остается проблема интерпретации. Ты знаешь, что кроме одного, по-моему хорошего, параграфа в Grundbegriffe я ничего не напечатал относительно связи аксиоматики теории вероятностей с реальным смыслом понятия вероятность, хотя и мог бы сделать это получше многих, и в докладах в Математическом обществе говорил на эту тему очень много. [9]
На втором - подобные области в предварительно облученном стержне. [10]
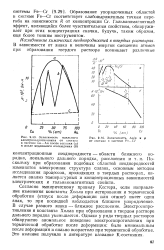 |
Зависимость удельного электросопротивления от состава ь системе Си - Аи после закалки ( а я после медленного охлаждения ( б.| Зависимость Ар / р и р от состава в системе Fe-Сг. [11] |
Поскольку при образовании подобных областей неоднородностей изменяется электронная структура сплава, основным методом исследования процессов, проходящих в твердых растворах, является анализ температурных и концентрационных зависимостей электрических и гальваномагнитных свойств. [12]
Наиболее правдоподобным объяснением возникновения подобных областей является предположение, чад метеоры, которые привели к появлению этих морей, до сих пор покоятся под их поверхностью - а эти метеоры имеют значительно большую плотность, чем каменистый материал, который обычно составляет лунную кору. По крайней мере дюжина масконов была обнаружена в пределах года после открытия первого из них. [13]
В случае уравнений гиперболического типа подобная область может быть описана с использованием характеристик исходного уравнения. Последние часто имеют достаточно сложный вид и, кроме того, могут зависеть от искомого решения. Поэтому при использовании простейших разностных схем, рассматриваемых ранее, не всегда оказывается учтенным высказанное выше требование. Более подходящим в таких случаях может быть численное интегрирование вдоль характеристик, которое и лежит в основе одноименного метода. При этом обычно используется сетка характеристик или аппроксимирующая ее сетка. В тех случаях, когда характеристики зависят от искомого решения, построение такой сетки приходится проводить одновременно с нахождением решения. Подобная организация вычислений позволяет достаточно точно определять область влияния исходных данных и, следовательно, строго учитывать распространение возмущений, что придает методу характеристик четкий физический смысл. Ниже мы изложим основную идею этого метода на примере задачи Коши для квазилинейного уравнения второго порядка гиперболического типа. [14]
Неймана структура, Беренса - Фишера проблема, Подобная область. [15]
Страницы: 1 2 3 4
