Анализ - корень - характеристическое уравнение
Cтраница 1
Анализ корней характеристического уравнения показывает, что в зависимости от значения Л412 переходной процесс нарастания напряжения может быть как апериодическим, так и колебательным. [1]
Анализ корней характеристического уравнения показывает, что их пары р1) 2 и р3 4 сильно отличаются друг от друга. [2]
Анализ корней характеристического уравнения Q ( р) 0 позволяет убедиться, что при одинаковых параметрах валопроводов оно содержит чисто мнимые корни, свидетельствующие о возможности незатухающих колебаний в рассматриваемой электромеханической системе. Эти корни удается определить путем разложения характеристического уравнения на множители. [3]
Общим методом определения границ зон самовозбуждения может служить анализ корней характеристического уравнения, полученного из системы уравнений Горева - Парка для рассматриваемой системы, содержа щей емкость. [4]
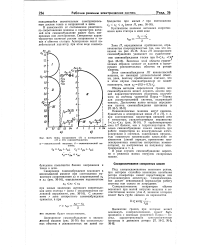 |
Зоны синхронного ( / и асинхронного ( / / и Ш самовозбуждения. [5] |
Общим методом определения границ зон самовозбуждения может служить анализ корней характеристического уравнения, полученного из системы уравнений Парка - Горева для рассматриваемой системы, содержащей емкость. [6]
 |
К понятию устойчивости состояний системы шар-поверхность. [7] |
Более строгая оценка устойчивости динамических систем может быть произведена на основе анализа корней характеристического уравнения. [8]
Критерии устойчивости формулируют необходимые и достаточные условия статической устойчивости, основанные на анализе корней характеристического уравнения, но не требующие их вычисления. [9]
В исследовании И. А. Вышнеградского был рассмотрен вполне конкретный вопрос - задача об устойчивости регуляторов2), Ценность этого исследования заключается в том, что И. А. Выш-неградский впервые применил к решению важного технического вопроса совершенную методику, основанную на анализе корней характеристического уравнения, составленного для системы дифференциальных уравнений колебательного движения регулятора. Эту систему уравнений И. А. Вышнеградский приводит к одному уравнению. [10]
Таким образом, можно сделать вывод, что одно и то же устройство - двигатель - может быть представлено апериодическим или колебательным звеньями в зависимости от соотношения между постоянными времени. На основании анализа корней характеристического уравнения колебательного звена, выполненного ранее, можно утверждать, что если нельзя пренебречь электромагнитной постоянной времени двигателя Та по сравнению с его электромеханической постоянной времени ГЭм при выполнении условия Там2Т9, то двигатель следует рассматривать как апериодическое звено второго порядка. [11]
При решении на АВМ незнакомых задач, а также при решении некоторых расчетных задач время решения или длительность переходного процесса часто бывают неизвестны. Для выбора масштаба времени необходим анализ корней характеристического уравнения моделируемой системы. АВМ уравнения обычно должны быть в пределах 0 1 - 10, что согласуется также с требованиями удобства и точности набора коэффициентов на блоках АВМ. [12]
Критерии устойчивости, подробно описанные в [3], классифицируются как прямые, требующие нахождения корней характеристического уравнения, и как косвенные, не требующие вычисления корней. Критерии устойчивости формулируют необходимые и достаточные условия устойчивости, основанные на анализе корней характеристического уравнения, но не требующие их вычисления. [13]
Если хотя бы один вещественный корень или вещественная часть комплексного корня положительны, то при т - оо приращение Д6 - оо и движение неустойчивое. Таким образом, области устойчивой и неустойчивой работы могут быть определены путем анализа корней характеристического уравнения исходной системы уравнений. [14]
Если хотя бы один вещественный корень или вещественная часть комплексного корня положительны, то при t - - се, Д6 - - оо и движение становится неустойчивым. Таким образом, области устойчивости и неустойчивости работы могут быть определены путем анализа корней характеристического уравнения исходной системы уравнений. [15]
Страницы: 1 2