Анализ - массообмен
Cтраница 1
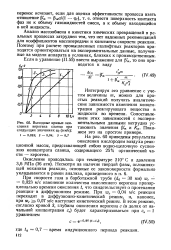 |
Выходные кривые окисления керогена сланца при следующих значениях ог ( вм / с. [1] |
Анализ массообмена и кинетики химческих превращений в реальных процессах затруднен тем, что нет надежных рекомендаций для коэффициентов массопередачи и константы скорости реакции. Поэтому при расчете промышленных газлифтных реакторов приходится ориентироваться на экспериментальные данные, полученные на модели аппарата в условиях, близких к производственным. [2]
Отметим, что при анализе массообмена газового пузыря с ялот-ной фазой псевдоожиженного слоя обычно предполагается, что число Пекле Ре гь ( Иь - v0f) / D, где D - эффективный коэффициент диффузии целевого компонента, много больше единицы. При таком предположении массоперенос происходит в пределах тонкого диффузионного пограничного слоя. В первой работе рассматривается массообмен пузыря с плотной фазой как при больших, так и при малых числах Пекле, а во второй - случай малых чисел Пекле. Однако, по мнению авторов работы [142], вывод о возможности существования малых чисел Пекле основан на неправильной оценке эффективного коэффициента диффузии. [3]
Еще одна трудность возникает при анализе массообмена между газом ( паром) и жидкостью. [4]
К сожалению, пронеденный при этом анализ массообмена носит сугубо эмпирический характер, а полученные уравнения не могут быть признаны достаточно надежными для использования их при решении разнообразных задач разделения. [5]
В предыдущих разделах данной главы при анализе массообмена газового пузыря с плотной фазой псевдоожиженного слоя предполагалось, что целевой компонент не вступает в химическую реакцию в плотной фазе слоя и не адсорбируется твердыми частицами. Поэтому изложенные в этих - разделах результаты можно применять при математическом моделировании химических реакторов или тешюмассообменных аппаратов с псевдоожиженным слоем только в том случае, если протекание химической реакции или адсорбционного процесса существенно не влияет на скорость массообмена газового пузыря с плотной фазой слоя. Цель данного раздела - построение математической модели массообмена газо - вого пузыря с плотной фазой псевдоожиженного слоя при наличии химической реакции. [6]
Полученное решение может быть использовано также для анализа массообмена изолированного пузыря со средой в лабораторных реакторах, когда ввод пузыря IB однородный псевдоожиженный слой осуществляется при помощи специального устройства на значительном расстоянии от входа в реактор. Влияние входного участка в этом случае незначительно, время формирования пузыря мало, распределение концентрации в начальный момент заметно отличается от (1.127) лишь на малых расстояниях от пузыря и решение пригодно до членов О ( Ре2) включительно. [7]
Полученное решение может быть использовано также для анализа массообмена изолированного пузыря со средой в лабораторных реакторах, когда ввод пузыря ( в однородный псевдоожиженный слой осуществляется при помощи специального устройства на значительном расстоянии от входа в реактор. Влияние входного участка в этом случае незначительно, время формирования пузыря мало, распределение концентрации в начальный момент заметно отличается от (1.127) лишь на малых расстояниях от пузыря и решение пригодно до членов О ( Ре2) включительно. [8]
Этот процесс осуществляется по схеме, изображенной на рис. 10.32 и 13.15. Анализ массообмена по этой схеме для различных технологических ситуаций проведен в разд. [9]
Для обработки лабораторных экспериментов по определению коэффициента диффузии экстрагируемого вещества в твердом теле, при анализе массообмена в промышленных экстракторах и других интервальных ( в том числе и инженерных) расчетах процесса экстракции могут быть широко использованы номограммы. [10]
В проведенных экспериментах пузыри воздуха, обогащенного озоном, инжектировались внутрь слоя и по измеренным значениям скорости разложения озона как функции размера пузырей была получена количественная информация об интенсивности массообмена между пузырями и плотной фазой. На основании этих данных был сделан вывод о том. Последнее подтверждает правильность применения модели конвективной диффузии для анализа массообмена между пузырем и непрерывной фазой в условиях, близких к минимальному псевдоожижению. [11]
Весьма важные для химической технологии массообменные процессы происходят в системах с капельными жидкостями. Это процессы растворения и экстрагирования, кристаллизации, жидкостной адсорбции, для которых значения критериев Прандтля оказываются существенно больше единицы. При этом конвективный перенос целевого компонента становится сравнимым с диффузионным на таких малых расстояниях от твердой поверхности, на которых характер течения потока капельной жидкости практически еще полностью определяется только силами вязкого трения, а толщины гидродинамического и диффузионного пограничных слоев становятся существенно неодинаковыми. Для капельных жидкостей, имеющих величины диффузионных критериев Прандтля порядка 103, диффузионный пограничный слой имеет приведенную толщину, значительно меньшую, чем гидродинамический пограничный слой, что в значительной мере упрощает анализ процесса внешнего массообме-на, поскольку при решении уравнения конвективно-диффузионного переноса компонента (1.21) в таком случае возможно воспользоваться приближенными решениями (1.7) для компонент скорости wx и wy, справедливыми для малых расстояний от стенки. Кроме того, при анализе массообмена твердой поверхности с потоками капельных жидкостей обычно предполагается пренебрежимо малое значение стефановского потока. [12]
Следовательно, когда G - и 5-точки располагаются на S-линии, точка G должна лежать немного правее этой линии, чему отвечает область в более высокой части градирни. Точка состояния основной массы газа находится в области смешанной фазы. Значит, в потоке газа могут содержаться мельчайшие капельки в виде тумана. Это обстоятельство делает несколько сомнительным справедливость и применимость развитых выше методов анализа массообмена. По-видимому, до сих пор не было проведено ни одного систематического исследования влияния смешанной фазы на соответствующие проводимости и дви жущие силы тепло - и массопереноса. Однако вряд ли приходится сомневаться в том, что ошибки от пренебрежения этим влиянием в задачах типа примера 7 - 11 практически окажутся совершенно незна Читель-ными. [13]
В результате оказывается вбзмож-ным получить выражения для компонент поля скорости газа, входящих в уравнение конвективной диффузии. Следующий этап описания массообмена пузыря с плотной фазой заключается в решении уравнения - дифуфузии. Отметим, что движение газовой и твердой фаз слоя и перенос тепла и массы в слое, вообще говоря, оказывают взаимное влияние друг на друга. Однако в целях упрощения анализа обычно предполагают, что влиянием тепло-и массообменных процессов на движение фаз можно пренебречь. В этом случае задача теоретического анализа тепло - или массо-обменного процесса разбивается на две задачи. Первая задача представляет собой теоретический анализ движения фаз в псевдоожи-женном слое, а вторая задача - анализ переноса тепла или массы. Как уже говорилось выше, на процессы переноса тепла или массы в псевдоожиженном слое может существенно влиять тепло-или массообмен газовых пузырей с плотной фазой слоя. При анализе массообмена газового пузыря с плотной фазой слоя также возникает целый ряд проблем. [14]
Страницы: 1