Математическая бесконечность

Cтраница 1

Математическая бесконечность) и резко выступал против теории множеств Кантора. [1]

Математическая бесконечность) впопъ - хотя и не в непосредственно наглядной форме - проникает в математику, коль скоро мы отказываемся от этой абстракции и пользуемся лишь абстракцией потенциальной осуществимости ( см. также Интуиционизм, Конструктивное направление), такое генетич. Обобщения этого метода применимы и по отношению к таким частично упорядоченным множествам, каждое линейно упорядоченное множество к-рых вполне упорядочено. [2]

Логицизм, Логический атомизм, Математическая бесконечность, Парадокс, Типов теория и лит. [3]

Здесь нет возможности сколько-нибудь полно осветить различные точки зрения на природу математической бесконечности, которые высказывались предшественниками Эйлера. Мы ограничимся поэтому тем, что нам кажется безусловно необходимым для понимания позиций нашего автора. [4]

Эти исследования ( см. Метод аксиоматический, Типов теория, Интуиционизм, Математическая бесконечность) оказывают значит, влияние на разработку логич. [5]

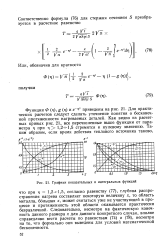Графики показательных и интегральных функций. [6]

Следовательно, несмотря на фактическую конечность данного размера х для данного конкретного случая, вполне справедливо вести расчеты по равенствам ( 74) и ( 78), несмотря на то, что формально они выведены для условий математической бесконечности. [7]

Рассмотрим is качестве примера поликонденсацию-четырехфуик-ционально го ( например, диамина) и бифункционального ( например, диэпоксида) соединения. Заметим, что это математическая бесконечность, так как реально количество молекул мономера в любой системе ограничено. [8]

Каждая из указанных выше формальных теорий имеет определ. Конструктивное направление, Логицизм, Математическая бесконечность, Математическая логика, Метод аксиоматический, Минимальная логика, Номинализ. [9]

Как известно, природа бесконечного была предметом различных толкований и многих дискуссий. Гильберт, считали, что математическая бесконечность не существует в природе и представляет собой некоторое условное понятие. В отличие от такой точки зрения Граве считал, что математическая бесконечность имеет объективный характер, прообразом ее является реальная физическая бесконечность материи. [10]

Есть и другой способ истолкования возможности практического применения бесконечно малых, и мы этим способом также будем пользоваться. Именно, практическая бесконечность различается от математической бесконечности. [11]

Чтобы понять смысл предложений ( у) Т1 ( х, х, у), требуются только понятие одного индивидуального эффективно вычислимого ( на самом деле даже примитивно - рекурсивного) предиката и понятие конструктивно1) применяемого квантора общности. Трудно себе представить более слабые предложения о наличном объеме понятий, коль скоро допускается какая бы то ни было математическая бесконечность. [12]

Второе характерное ограничение теории несущих линий касается стреловидности крыла, особенности, которая принята на высокоскоростных самолетах по причинам, подробнее объясненным нами в главе IV. Если мы заменим стреловидное крыло на стреловидную несущую линию, то расчет скоса потока окажется очень трудным, потому что возникают математические бесконечности на несущей линии. [13]

Каждый из третичных атомов углерода в соединениях 15 является асимметрическим центром. Ла их синтез ( по 1мг) не хватит уже всех нуклонов во всей наблюдаемой Все-лепной. Так, от абстрактной математической бесконечности мы приходим к вполне реальной, истинной неисчерпаемости многообразия возможных органических соединений. [14]

Возражая против концепции актуально бесконечно малых, он далее пишет: Невозможно ничему непрерывному состоять из неделимых частей, например линии из точек, если линия непрерывна, а точка неделима. Взгляды Аристотеля в отношении математической бесконечности не были лишены противоречий. Сознавая большие трудности, связанные с понятием бесконечности и с разрешением апорий Зенона, Аристотель пытался найти выход и как-то обосновать разрыв между непрерывностью и дискретностью. Он выступал против пользования понятием движения в математике, мотивируя это тем, что эта наука занимается не самими реальными вещами, а лишь абстракциями от них. [15]

Страницы: 1 2