Обозначение - шенфлис
Cтраница 1
Обозначения Шенфлиса применяются, в основном, для описания симметрии точечных групп и макрофизических свойств кристаллов. Международные обозначения используются для описания пространственных групп и в структурном анализе кристаллов. [1]
Каждая пространственная группа дается как в обозначениях Шенфлиса, так и в интернациональных символах. Группы даются в установке, удовлетворяющей трем правилам Бравэ. Если интернациональный символ, проставленный в таблице, отличается по виду от того, который используется обычно в структурных справочниках, последний указывается добавочно в скобках. [2]
В квантовой химии для молекулярных точечных групп и операций симметрии применяются обозначения Шенфлиса. Операция инверсии, которая переводит каждую точку в симметричную ей относительно начала координат точку, обозначается через i. [3]
В табл. 3 приведены все 230 пространственных групп симметрии в старой системе обозначений Шенфлиса, а также в новейшей системе Германа - Могена. Символы учитывают основные, но, конечно, не все имеющиеся элементы симметрии. Заглавная буква в начале символа обозначает тип решетки Бравэ. [4]
Теперь можно объяснить основные правила, которыми выражают симметрию молекул, используя соответствующие обозначения. Воспользуемся обозначениями Шенфлиса, так как их наиболее часто применяют для молекул спектроскописты, химики и физики. Кристаллографы обычно используют другой набор обозначений, основанный на несобственном вращении, которое определено иным образом. [5]
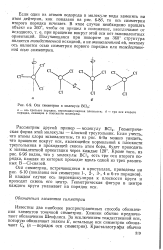 |
Оси симметрии в молекуле ВС13. [6] |
Известны два наиболее распространенных способа обозначения элементов точечной симметрии. Химики обычно предпочитают обозначения Шенфлиса. [7]
Таким образом, свойства симметрии молекулы можно описать, перечислив все ее возможные операции симметрии, при которых молекула с физической точки зрения остается неизменной. Для этого используются простые символы ( обозначения Шенфлиса), указывающие важнейшие группы симметрии. [8]
Молекулы можно классифицировать в группы симметрии по числу и характеру элементов симметрии, которыми эти молекулы обладают. В молекулярной спектроскопии для описания 32 возможных групп симметрии ( точечных групп) наиболее часто используются обозначения Шенфлиса; в кристаллографических работах используются системы Герман-Могена. Ниже приводятся обозначения Шенфлиса для точечных групп симметрии и соответствующие элементы симметрии. [9]
Молекулы можно классифицировать в группы симметрии по числу и характеру элементов симметрии, которыми эти молекулы обладают. В молекулярной спектроскопии для описания 32 возможных групп симметрии ( точечных групп) наиболее часто используются обозначения Шенфлиса; в кристаллографических работах используются системы Герман-Могена. Ниже приводятся обозначения Шенфлиса для точечных групп симметрии и соответствующие элементы симметрии. [10]
В кристаллографии для обозначения точечной симметрии используют систему Германа-Могена. Эта система обозначений была использована в гл. Однако в инфракрасной спектроскопии и различных других областях химии предпочитают систему обозначений Шенфлиса. [11]
Группы Sn включают зеркальные повороты вокруг зеркально-поворотной оси л-го порядка. Для нечетных п они совпадают с группами Dn. Как уже было сказано, в международной символике зеркально-поворотной оси п отвечает поворот на угол ( 2jt /) / k с последующей инверсией. Она соответствует группе 82лв обозначениях Шенфлиса. [12]
В таблицах принято обозначать через L более длинную ось, а через М - более короткую ось, которые лежат в плоскости. В большинстве случаев это определение однозначно, так как указанные оси являются также осями симметрии. В коронене М - ось, проходящая через максимальное число атомов, а в хризене L - ось, параллельная максимальному числу связей. В бензоле использовано другое условие, о чем сказано в пояснении к таблице. Когда это целесообразно, для получения системы неэквивалентных осей выбрано, как обычно, преобразование, указанное в обозначениях Шенфлиса. [13]
Страницы: 1