Тороидальная оболочка

Cтраница 2

Ветвление решений нелинейных уравнений тороидальных оболочек при действии внешнего давления / / Прикл. [16]

Применим уравнение (10.133) к тороидальной оболочке. [17]

Таким образом, эквивалентная оптимальной тороидальная оболочка кругового поперечного сечения оказывается примерно на 30 % более материа-лоемкой. [18]

Сравнение полученных результатов при загружеиии тороидальной оболочки локальной нагрузкой в зонах различной гауссовой кривизны позволяет сделать вывод, что распределение компонент тензора напряжений по толщине имеет нелинейных характер. Это явление особенно характерно для случая действия локальной нагрузки в области отрицательной гауссовой кривизны. [19]

Детали конструкций, имеющие форму тороидальной оболочки, применяются в машиностроении достаточно часто. [20]

Диаграмма условных т. 1 17 для вогнутой стороны И / И напряжений растянутого во - Q g выпуклой. [21]

Феппля, определяющая напряжения безмоментного состояния тороидальной оболочки. [22]

Сильфоны представляют собой составную конструкцию из тороидальных оболочек, поэтому развитие методов расчета сильфонов следует продвижениям в теории тороидальных оболочек. [23]

Известно, что напряженное осесимметричное состояние тороидальной оболочки описывается системой обыкновенных дифференциальных уравнений четвертого порядка. Если свести систему уравнений к одному дифференциальному уравнению и представить, как обычно, решение в виде суммы общего решения однородного уравнения и частного решения, соответствующего заданной правой части, то решение однородного уравнения будет определять напряженное состояние краевого эффекта, частное же решение с достаточной точностью опишет безмоментное напряженное состояние. [24]

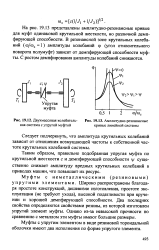Двухмассовая колебательная система с упругой муфтой.| Амплитудно-резонансные кривые линейной системы. [25]

Муфты с упругим элементом в виде резиновой тороидальной оболочки имеют два исполнения по форме упругого элемента. [26]

На рис. 4.16 показаны формы образующей круговой незамкнутой тороидальной оболочки ( 2оо2л / 3), подверженной действию внутреннего равномерно распределенного давления. [27]

Зазор между внешней поверхностью первого сегмента ( тороидальная оболочка - впадина) и кольцом до нагружения равен нулю. [28]

Таким образом, устойчивость процесса упругопластического деформирования тороидальной оболочки, находящейся под действием внутреннего давления, определяется эллиптичностью ее поперечного сечения. Тороидальные оболочки с малой эллиптичностью поперечного сечения ( 1 0& 1 6) за пределом упругости воспринимают дальнейшее повышение нагрузки. Увеличение эллиптичности поперечного сечения тороидальных оболочек ( &16) приводит к тому, что переход в пластическое состояние сопровождается потерей их несущей способности. [29]

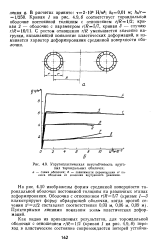Упругопластическая неустойчиоость круговых тороидальных оболочек. [30]

Страницы: 1 2 3 4 5