Коническая оболочка
Cтраница 3
Расчет конических оболочек с учетом осе-симметричных и обратносимметричных температурных воздействий приведен в гл. Вопросы расчета оболочек произвольного очертания на температурные воздействия рассматриваются также в гл. [31]
Анализ конических оболочек требует введения специальной системы координат, отличной от той, которая была - принята в разделе IVA для оболочки вращения двойной кривизны. В теории конических оболочек используются две системы координат: 1) традиционные коцические координаты; 2) усеченные конические координаты. [32]
Расчеты конических оболочек значительно упрощаются, если они могут быть отнесены к длинным оболочкам. [33]
Устойчивости конических оболочек с несимметричным расположением слоев уделялось удивительно мало внимания. [34]
Колебания конических оболочек с ортотропными несущими слоями были впервые рассмотрены Азаром [21], который применил метод Релея - Ритца для исследования осесимметричных ч колебаний оболочек со свободно опертыми краями. Бейкон и Берт [23] распространили этот анализ на неосесимметричные формы колебаний. [35]
Для безмоментной конической оболочки краевые меридиональ ные усилия имеют вид ( см. гл. [36]
Задача устойчивой конической оболочки за пределом упругости материала значительно сложнее задачи устойчивости цилиндрической оболочки, так как докритическое напряженное состояние неоднородно. [37]
Устойчивость многослойной композитной конической оболочки при равномерном внешнем давлении / / Прикл. [38]
Для замкнутой усеченной конической оболочки ( хг х х2 I xt), опертой по краям, решение уравнений ( 46) проще всего искать, используя метод Галеркина. [39]
Для сферических и конических оболочек с большим подъемом каждое дифференциальное уравнение может быть преобразовано в дифференциальное уравнение четвертого порядка с постоянными коэффициентами. [40]
Испытания тщательно изготовленных замкнутых и усеченных конических оболочек при внешнем давлении показывают, что потеря устойчивости сопровождается хлопком. [41]
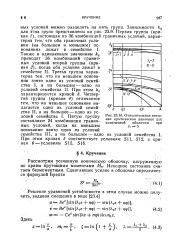 |
Относительное внешнее критическое давление для конической оболочки при. [42] |
Рассмотрим усеченную коническую оболочку, нагруженную по краям крутящими моментами Мк. Исходное состояние считает безмоментным. [43]
Рассмотрим далее коническую оболочку под действием внесшего равномерного поперечного давления. Начальное состояние считаем беэ-моментным. [44]
Рассмотрим теперь коническую оболочку постоянной толщины, нагруженную равномерным давлением. [45]
Страницы: 1 2 3 4