Толстостенная цилиндрическая оболочка
Cтраница 1
Толстостенные цилиндрические оболочки и кольца, образуемые методой намотки, находят широкое применение в конструкциях самого разнообразного назначения. Основная особенность расчета и проектирования толстостенный композитных элементов связана с необходимостью анализа их напряженного состояния на этапе изготовления, так как возникающие при этом начальные технологические напряжения оказывают существенное ( а иногда и решающее) влияние на несущую способность. [1]
Для практического расчета толстостенной цилиндрической оболочки, находящейся в сложном напряженном состоянии, необходимо заменить совместное действие трех главных напряжений af, аг и ог эквивалентным им действием растягивающего напряжения тэ; эта замена осуществляется при помощи теорий прочности. [2]
Ламе, для диска или толстостенных цилиндрических оболочек, нагруженных равномерно распределенным внутренним и внешним давлениями. Ламе с целью проверки сходимости и точности, которую можно провести с теми немногими членами ряда, который дается в указанных выражениях. [3]
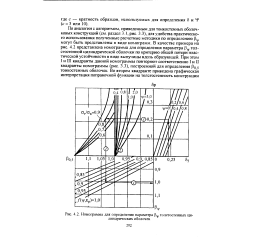
В качестве примера на рис 42 представлена номограмма для определения параметра [ 3 толстостенной цилиндрической оболочки по критерию общей потери пластической устойчивости в виде выпучины вдоль образующей. При этом I и III квадранты данной номограммы повторяют соответственно I и II квадранты номограммы ( рис. 3.3), построенной для определения fig 5 тонкостенных оболочек. [4]
Некоторые решения, основанные на использовании полей локальных напряжений, были получены для толстостенных цилиндрических оболочек, например для случая осесимметричного напряженно-деформированного состояния), а приближенное решение было получено для сплошного цилиндра 2) и может быть использовано для полых цилиндров или применено к ним путем вычитания решений для толстостенного цилиндра, и для отверстия. [5]
В настоящем разделе предлагается методика оценки несущей способности рассматриваемых сферических конструкций ( см. рис. 4.1 6), базирующаяся на концентрациях и допущениях, принятых ранее при анализе толстостенных цилиндрических оболочек. [6]
 |
Принципиальная схема испытания кольцевых образцов-моделей в условиях действия наружного ( а и внутреннего ( б давления. [7] |
Кроме того, испытание данных кольцевых образцов в специальных контейнерах ( рис. 4.4) позволяет наиболее полно реализовать в них условия плоской деформации в направлении образующей кольца, которые имеют место в толстостенных цилиндрических оболочках при их нагру-жении внутренним или внешним давлением. Для обеспечения обжатия моделирующего образца, имитирующего нагруже-ние внешним давлением q, втулка располагается с его наружной поверхности, а для осуществления раздачи образца, моделирующей его нагру-жение внутренним давлением р, - внутри образца. [8]
 |
Принципиальная схема испытания кольцевых образцов-моделей в условиях действия наружного ( а и внутреннего ( б давления. [9] |
Кроме того, испытание данных кольцевых образцов в специальных контейнерах ( рис. 4.4) позволяет наиболее полно реализовать в них условия плоской деформации в направлении образующей кольца, которые имеют место в толстостенных цилиндрических оболочках при их нагру-жснии внутренним или внешним давлением. [10]
Попутно отметим, что если TConst, то правая часть в (4.7) равна нулю и говорить о температурных напряжениях не приходится. Другими словами, температурные напряжения в толстостенных цилиндрических оболочках вызываются не температурой, а ее градиентом. [11]
 |
Номограмма для определения параметра Р толстостенных цилиндрических оболочек. [12] |
По аналогии с алгоритмом, приведенным для тонкостенных оболочковых конструкций ( см. раздел 3.1, рис. 3.3), для удобства практического использования полученные расчетные методики по определению Рц, могут быть представлены в виде номограмм. В качестве примера на рис. 4.2 представлена номограмма для определения параметра ( 3 толстостенной цилиндрической оболочки по критерию общей потери пластической устойчивости в виде выпучины вдоль образующей. При этом I и III квадранты данной номограммы повторяют соответственно I и II квадранты номограммы ( рис. 3.3), построенной для определения ( 30 тонкостенных оболочек. [13]
При холодной объемной штамповке на матрицы действует внутреннее давление со стороны штампуемого металла. В матрице возникают тангенциальные, радиальные и осевые напряжения, которые можно рассчитать по формулам Ляме как для толстостенных цилиндрических оболочек. Напряжения, возникающие в матрице при выдавливании, можно значительно уменьшить. Прочность матриц увеличивают напрессовкой на них бандажей с определенным натягом. В результате матрице сообщаются предварительные напряжения, по знаку противоположные напряжениям, возникающим при штамповке. По числу бандажей матрицы делят на одно - и многобандажные. Допустимые давления в случае однобяндажной матрицы определяются механическими свойствами материала бандажа и превышают предельно допустимое напряжение для этого материала приблизительно в 1 1 раза. [14]
Эти хвостовики или отковывают как одно целое с крайними дисками, или приваривают к дискам. Обычно цельнокованые хвостовики представляют собой толстостенные цилиндрические оболочки, а сварные - тонкостенные. [15]
Страницы: 1 2