Эллипсоидальная оболочка
Cтраница 1
Эллипсоидальная оболочка, заполненная жидкостью, равномерно вращается относительно некоторого заданного диаметра. Доказать, что траектория каждой частицы жидкости относительно эллипсоида будет эллипсом, плоскость которого является сопряженной заданному диаметру, и что каждая частица будет двигаться по своей эллиптической орбите так, что радиус-вектор, проведенный из центра орбиты, будет описывать равные площади в равные промежутки времени. [1]
Для вытянутой эллипсоидальной оболочки главные радиусы кривизны являются наибольшими в зоне экватора / ( рис. 36), где и следует ожидать появления вмятин. [2]
Практические расчеты эллипсоидальных оболочек надо вести по величине qH, значение которой составляет приблизительно такую же долю от qg, как и для сферических оболочек. [3]
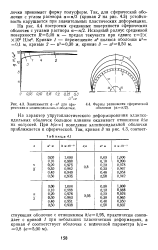 |
Зависимости q - us для сферических и эллипсоидальных оболочек. [4] |
При Ь / а - - поведение эллипсоидальной оболочки приближается к сферической. [5]
В работах [305 306] рассмотрены аналогичные задачи для пологих и эллипсоидальных оболочек. [6]
Рассмотрим задачу о действии локальной нагрузки на эллипсоидальную оболочку. [7]
 |
Формы образующей эллипсоидальной оболочки ( Ь / с 0 8 в процессе деформирования.| Расчетная схема цилиндрической оболочки. [8] |
Необходимо отмстить, что потеря устойчивости пологих сферических оболочек и эллипсоидальных оболочек с отношением й / с0 5 может произойти задолго до того, как нх срединная поверхность примет форму полусферы. Это объясняется значительным уменьшением толщины в полюсе таких оболочек. [9]
В пищевой и химической отраслях промышленности широко применяют эллиптические днища, представляющие собой половину сплющенной эллипсоидальной оболочки вращения. Задача об устойчивости эллипсоидальной оболочки, нагруженной внешним давлением, родственна задаче об устойчивости сферической оболочки. [10]
Таким образом, при увеличении эллиптичности поперечного сечения оболочки в направлении действия нагрузки или расширении зоны ее приложения перемещения и3 и напряжения о в эллипсоидальной оболочке уменьшаются. [11]
В пищевой и химической отраслях промышленности широко применяют эллиптические днища, представляющие собой половину сплющенной эллипсоидальной оболочки вращения. Задача об устойчивости эллипсоидальной оболочки, нагруженной внешним давлением, родственна задаче об устойчивости сферической оболочки. [12]
 |
Формы образующей эллипсоидальной оболочки ( Ь / с 0 8 в процессе деформирования.| Расчетная схема цилиндрической оболочки. [13] |
Изменение толщины происходит наиболее интенсивно в месте максимальных пластических деформаций - в полюсе оболочки. В таблице 4.1 приведены значения толщины сферических и эллипсоидальных оболочек в зависимости от перемещения полюса. [14]
В металлическом состоянии у технеция и рения, судя по их устойчивым валентностям 4, 6 и по более низким потенциалам ионизации, в свободное состояние могут переходить 5 внешних d - электронов. Число свободных электронов во всяком случае должно быть ниже, чем у молибдена и вольфрама ( 6), поскольку технеций и рений имеют более низкие температуры плавления. Образующиеся при этом ионы имеют эллипсоидальную оболочку из двух s - электронов и упаковываются в результате взаимодействия с электронным газом в плотную гексагональную структуру. На большую плотность электронного газа ( 5 эл / атом) указывает высокая термодинамическая устойчивость гексагональных структур технеция и рения, сохраняющихся вплоть до их весьма высоких температур плавления. Отметим, что при растворении в решетке молибдена или вольфрама атомы технеция и рения могут терять по семь валентных электронов и внешняя р - оболочка их ионов способствует образованию очень широких областей твердых растворов на основе объемноцентрированных кубических структур молибдена и вольфрама. Эти сплавы отличаются сочетанием высокой прочности и пластичности. [15]
Страницы: 1